На графіку відображено зміну робочої температури двигуна легкового автомобіля протягом 10 хвилин з моменту його запуску. Визначте за графіком кількість хвилин, протягом яких робоча температура двигуна була не більшою за 50 °С.
Зріст людини 6 футів 1 дюйм. Виразіть його ріст в сантиметрах, якщо 1 фут дорівнює 12 дюймів. Вважайте, що 1 дюйм дорівнює 2,54 см. Результат округліть до цілого числа в сантиметрах.
У скільки разів збільшиться об’єм кулі, якщо її радіус збільшити втричі?
Розв'яжіть рівняння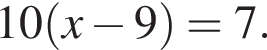
Різниця двох кутів, отриманих при перетині двох прямих (див. рисунок), дорівнює 120°. Визначте градусну міру кута а.
Графік функції, заданої формулою y = kx + b симетричний щодо початку координат і проходить через точку A (2; 10). Значення виразу k + b одно:
Спростіть вираз 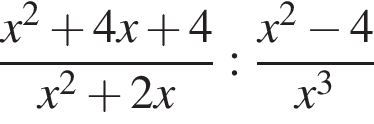 .
.
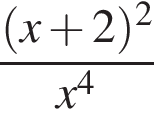
Доцентрове прискорення при русі по колу (м/c 2 ) можна обчислити за формулою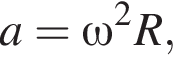 де
де![]() - Кутова швидкість (в -1 ), а R - радіус кола. Користуючись цією формулою, знайдіть відстань R (у метрах), якщо кутова швидкість дорівнює 3 с −1 , а доцентрове прискорення дорівнює 45 м/c 2 .
- Кутова швидкість (в -1 ), а R - радіус кола. Користуючись цією формулою, знайдіть відстань R (у метрах), якщо кутова швидкість дорівнює 3 с −1 , а доцентрове прискорення дорівнює 45 м/c 2 .
Укажіть проміжок, якому належить число ![]()
Які з таких тверджень вірні?
I. Якщо при перетині двох прямих третьою прямою відповідні кути дорівнюють 37°, то ці дві прямі паралельні.
ІІ. Через будь-які три точки проходить не більше однієї прямої.
ІІІ. Сума вертикальних кутів дорівнює 180°.
Якому проміжку належить корінь рівняння 
Знайдіть похідну функції 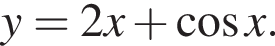
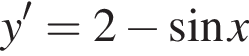
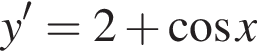
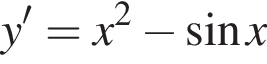
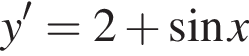
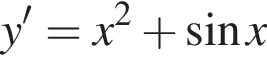
Розв’яжіть нерівність 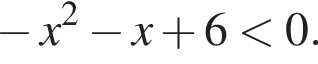
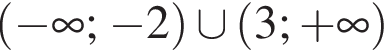
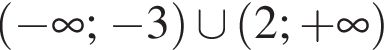

Знайдіть  якщо
якщо 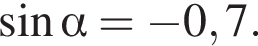
Діаметр основи конуса дорівнює 12, а довжина твірної — 10. Знайдіть площу осьового перерізу цього конуса.
На рисунку зображено ескіз емблеми. Емблема має форму кола радіуса 2 м, усередині якого розміщено 6 однакових півкіл. Один кінець кожного півкола збігається із центром кола, інший кінець лежить на колі. Для виготовлення емблеми (з усіма елементами включно) потрібен гнучкий матеріал вартістю 200 грн за 1 м довжини. Укажіть з-поміж наведених сум грошей найменшу, якої достатньо, шоб придбати цей матеріал для виготовлення емблеми. Уважайте, що на з'єднання елементів емблеми не потрібно додаткових витрат матеріалу.
До кожного початку речення (1−4) доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
1. Функція ![]()
2. Функція 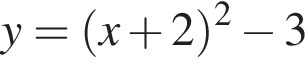
3. Функція 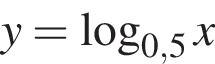
4. Функція 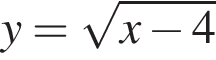
А набуває від'ємного значення в точці ![]()
Б не визначена в точці ![]()
В має екстремум у точці 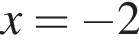
Г набуває додатного значення в точці 
Д є непарною
Установіть відповідність між запитанням (1−4) та правильною відповіддю на нього (А−Д).
1. Яке число є квадратом натурального числа?
2. Яке число є простим?
3. Яке число є дільником 8?
4. Яке число кратне 7?
А 8
Б 16
В 17
Г 27
Д 56
На рисунку зображено коло з центром у точці О, радіус якого дорівнює 6. Хорду ВС видно з центра кола під кутом 60°, ВК — діаметр. Через точку А до кола проведено дотичну АВ, причому АО=2АВ. Установіть відповідність між відрізком (1−4) та його довжиною (А−Д).
1. BK
2. AB
3. BC
4. CK
А ![]()
Б 6
В ![]()
Г ![]()
Д 12
На рисунку зображено куб АВСDА1B1C1D1. Установіть відповідність між парою прямих (1−4) та їх взаємним розташуванням (А−Д).
1 AC й CC1
2 AB1 i CD1
3 AC й CD1
4 AB1 i C1D
А прямі паралельні
Б прямі мимобіжні
В прямі перетинаються й утворюють прямий кут
Г прямі перетинаються й утворюють кут 45°
Д прямі перетинаються й утворюють кут 60°
У бібліотеці є лише підручники, словники, довідники та книги з художньої літератури. Відсотковий розподіл кількості цих книг у бібліотеці відображено на діаграмі.
1. Визначте загальну кількість книг у цiй бiблiотецi, якщо кiлькiсть пiдручникiв дорiвнює 72.
2. Скільки потрібно придбати додатково підручників, щоб отримана після цього їхня сумарна кількість відносилася до кількості довідників як 4:1?
На рисунку зображено квадрат АВСD, сторона якого дорівнює 15. На сторонах АD і ВС квадрата вибрано точки К i М так, що АК = 4, МС = 3.
1. Визначте вiдстань мiж серединами вiдрiзкiв AB i KM.
2. Обчислiть довжину вiдрiзка KM.
У прямокутній системі координат у просторі задано точки А(−7; 4; −3) і B(17; −4; 3). Точка С є серединою відрізка АВ.
1. Визначте абсцису точки С.
2. Обчислiть довжину (модуль) вектора ![]()
Арифметичну прогресію (an) задано формулою n-го члена: 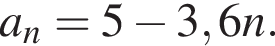
1. Визначте шостий член піеї прогресії.
2. Визначте різнищю 
Імовірність того, що на тестуванні з математики учень П. правильно вирішить більше 12 завдань, дорівнює 0,7. Імовірність того, що П. правильно вирішить більше 11 завдань, дорівнює 0,79. Знайдіть ймовірність того, що П. правильно вирішить рівно 12 завдань.
З двох міст, відстань між якими дорівнює 560 км, назустріч один одному одночасно виїхали два автомобілі. Через скільки годин автомобілі зустрінуться, якщо їхні швидкості дорівнюють 65 км/год та 75 км/год?
Обчисліть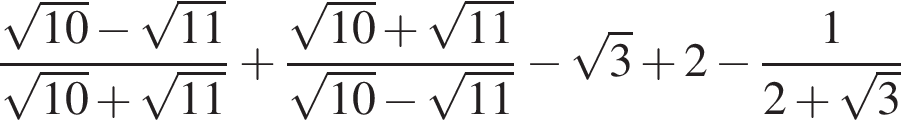 .
.
Розв'яжіть рівняння У відповіді запишіть добуток усіх його дійсних коренів.
У відповіді запишіть добуток усіх його дійсних коренів.
В Оленки є 8 різних фотографій з її зображенням та 6 різних фотографій її класу. Скільки всього в неї є способів вибрати з них 3 фотографії зі своїм зображенням для персональної сторінки в соціальній мережі та 2 фотографії свого класу для сайту школи?
| x | y |
|---|---|
| 0 | |
| 0 | |
| 9 |
Задано функцiю 
1. Для наведених у таблиці значень х та у заданої функції визначте відповідні їм значення у та х. Результати запишіть у таблицю.
2. Побудуйте графік функції 
3. Позначте на рисунку точки перетину графіка функції з осями координат та укажіть координати цих точок.
4. Знайдіть одну з первісних ![]() для функції
для функції 
5. Запишіть формулу для обчислення площі S фігури, обмеженої графіком функції f та осями координат.
6. Обчисліть площу S цієї фігури.
Сторона основи правильної трикутної піраміди дорівнює 4. Бічні ребра нахилені до основи під кутом α.
1. Зобразіть на малюнку цю піраміду та кут α.
2. Знайдіть бічне ребро піраміди.
3. Знайдіть площу повної поверхні піраміди.
Відповідно до умови завдання 31 (№ 3486) сторона основи правильної трикутної піраміди дорівнює 4. Бічні грані нахилені до основи під кутом β.
а) Зобразіть на малюнку цю піраміду та побудуйте лінійний кут двогранного кута при бічному ребрі.
б) Знайдіть цей кут.
Доведіть рівність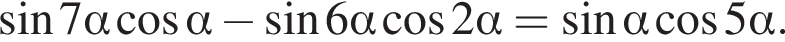
Задано рівняння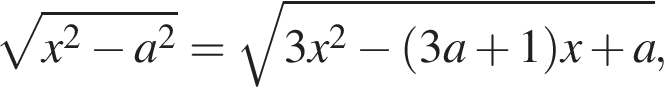 де x – змінна, a – параметр.
де x – змінна, a – параметр.
1. Розв'яжіть рівняння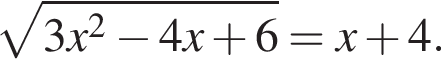
2. Знайдіть усі значення a , при кожному з яких рівняння має рівно один корінь на відрізку [0; 1].

 Из графика видно, что по прошествии трех минут температура составила 50 градусов и ниже уже не опускалась, поэтому ответ 3 минуты.
Из графика видно, что по прошествии трех минут температура составила 50 градусов и ниже уже не опускалась, поэтому ответ 3 минуты.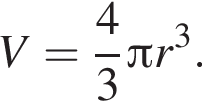


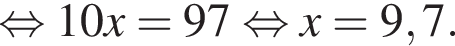

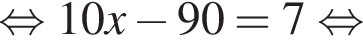
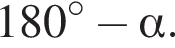 По условию
По условию 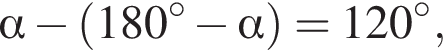 откуда
откуда 

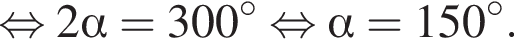
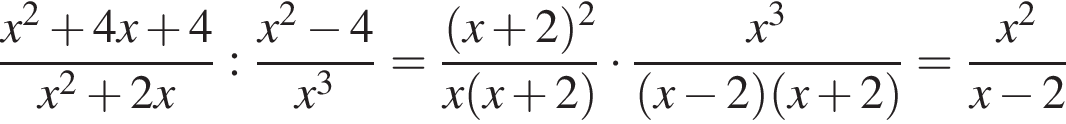
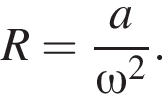 Подставим значения переменных a и
Подставим значения переменных a и 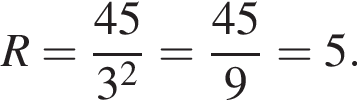

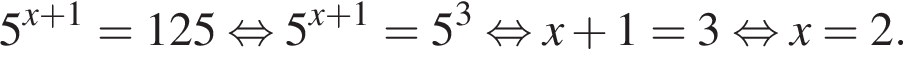

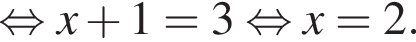

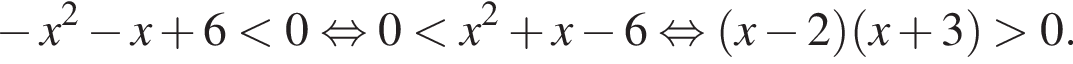

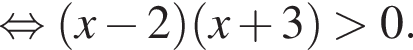
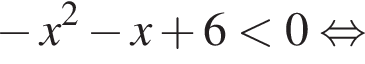
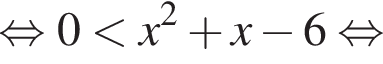
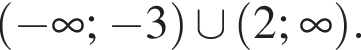
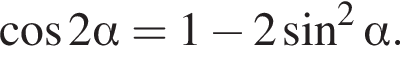 Получаем:
Получаем: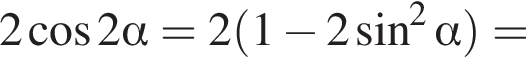
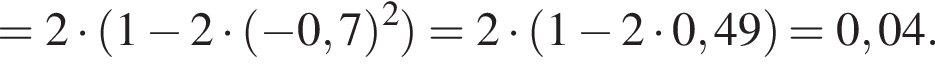
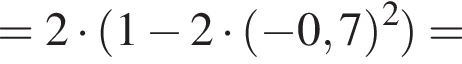
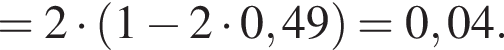
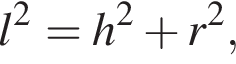 откуда
откуда 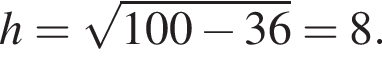 Следовательно, площадь осевого сечения равна 0,5 · 12 · 8 = 48.
Следовательно, площадь осевого сечения равна 0,5 · 12 · 8 = 48. метров, а длина полукругов — дополнительно
метров, а длина полукругов — дополнительно 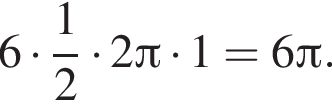 Итого требуется
Итого требуется  метров материала, который будет стоить
метров материала, который будет стоить 
 функция
функция  например, не выполняется или вообще не имеет смысла, поэтому других нечетных функций нет.
например, не выполняется или вообще не имеет смысла, поэтому других нечетных функций нет.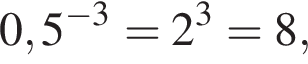 то
то 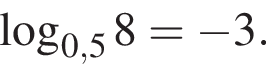 Прочие функции при
Прочие функции при 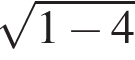 не определено. Прочие функции определены в точке 1
не определено. Прочие функции определены в точке 1 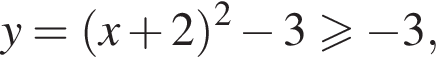
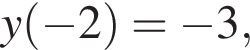 поэтому при
поэтому при 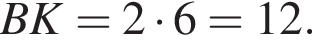 Таким образом, 1 — Д.
Таким образом, 1 — Д. 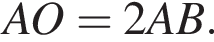 Применив теорему Пифагора, получим:
Применив теорему Пифагора, получим: 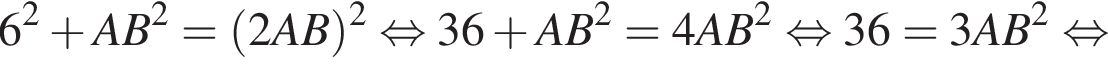
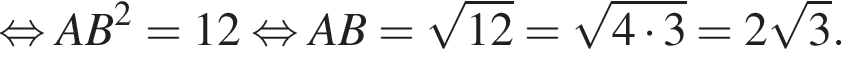
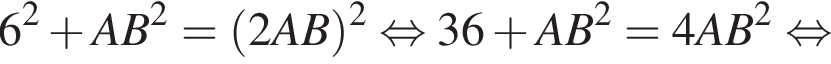


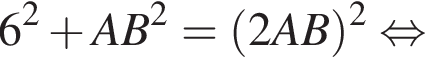
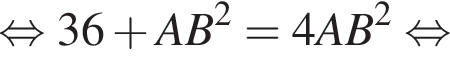
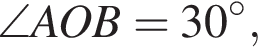 получим такой же результат, так как известно, что гипотенуза вдвое больше катета, противолежащего углу, градусная мера которого равна 30°. Найдем AB:
получим такой же результат, так как известно, что гипотенуза вдвое больше катета, противолежащего углу, градусная мера которого равна 30°. Найдем AB: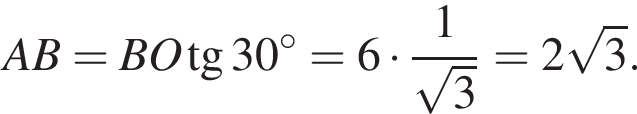

 поэтому треугольник BOC — равносторонний. Отсюда BC = 6, таким образом, 3 — Б.
поэтому треугольник BOC — равносторонний. Отсюда BC = 6, таким образом, 3 — Б. 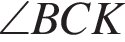 опирается на диметр окружности, поэтому
опирается на диметр окружности, поэтому  отсюда BCK — прямоугольный. Так как BK = 12,
отсюда BCK — прямоугольный. Так как BK = 12,  найдем CK:
найдем CK: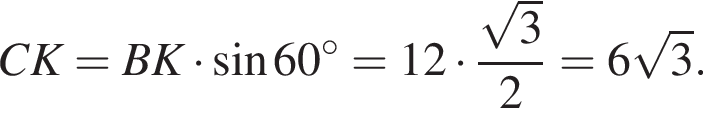

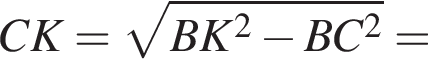

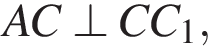 потому что
потому что 
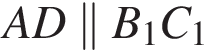 как ребра параллелепипеда и
как ребра параллелепипеда и  Значит, AB1C1D — параллелограмм, поэтому
Значит, AB1C1D — параллелограмм, поэтому 
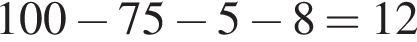 процентов от общего числа книг. По условию
процентов от общего числа книг. По условию 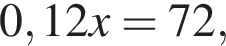 откуда
откуда 
 справочников, поэтому учебников должно стать
справочников, поэтому учебников должно стать 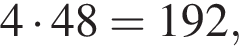 значит нужно докупить еще
значит нужно докупить еще  учебников.
учебников.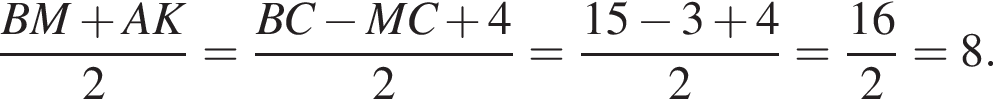
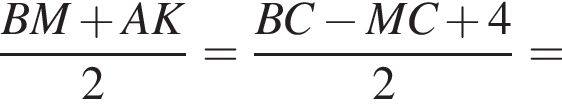
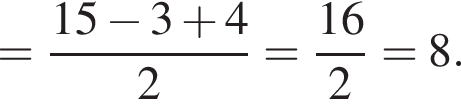

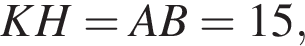
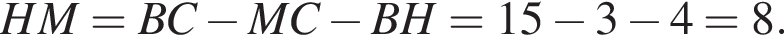

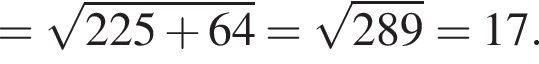

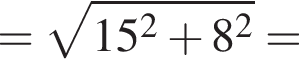
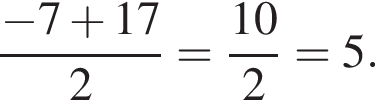
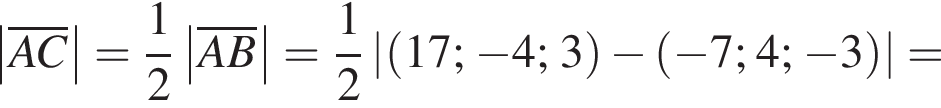
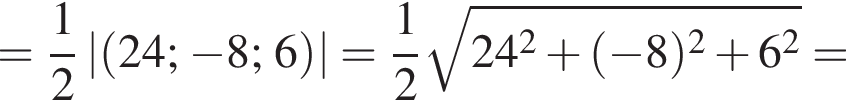
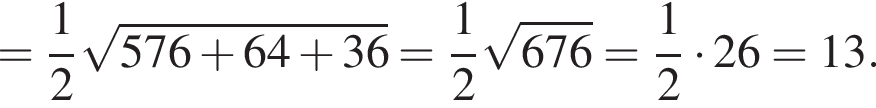
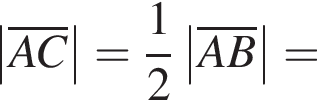
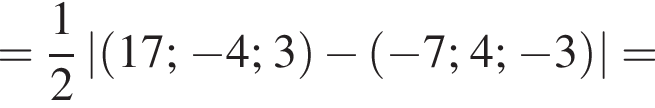
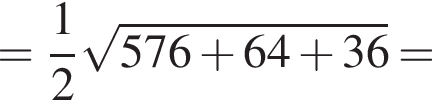
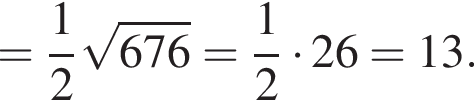
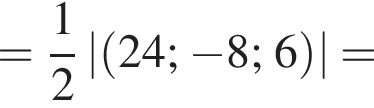
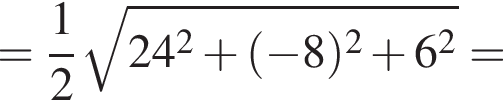
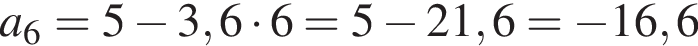
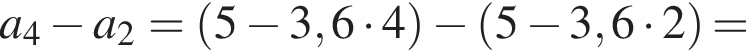

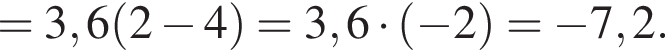
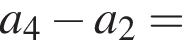

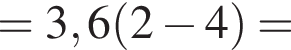
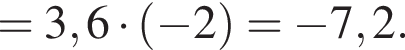
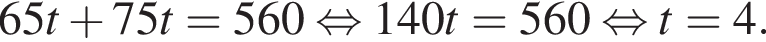
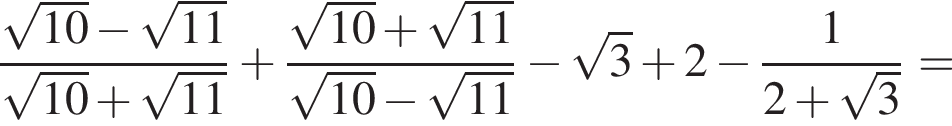
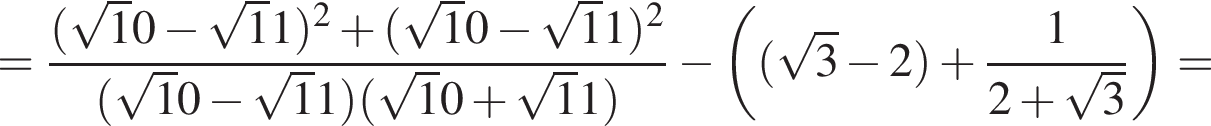
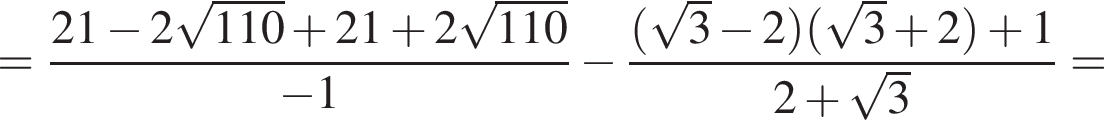
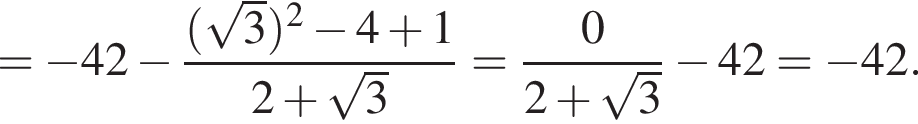
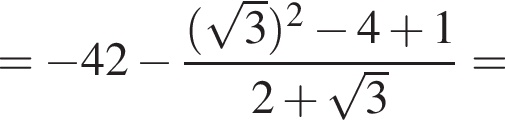
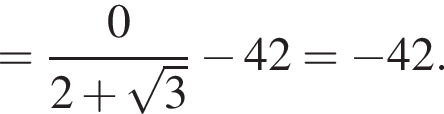
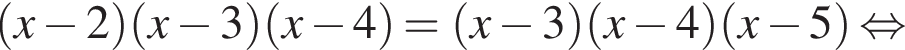
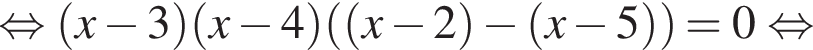
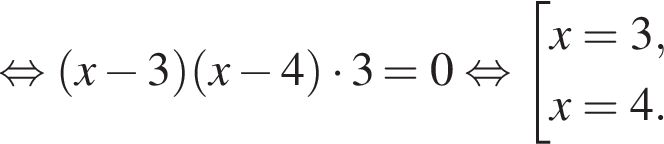
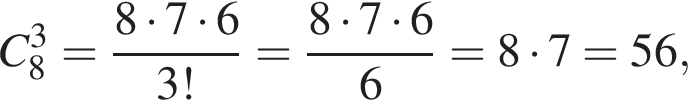
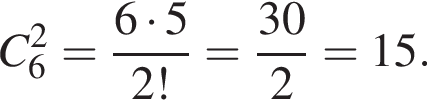
 способов.
способов.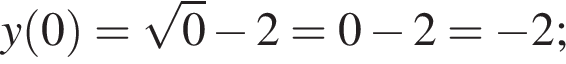
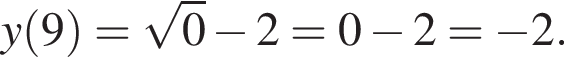

 сдвинутый вниз на 2.
сдвинутый вниз на 2.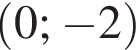 и
и 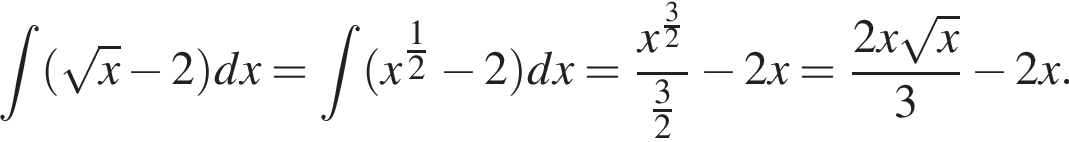
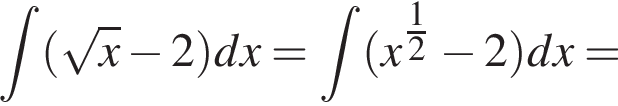
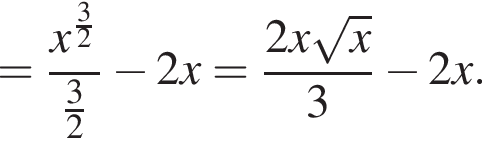
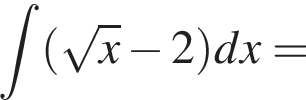
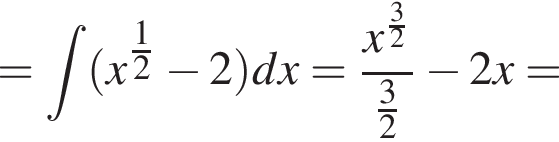
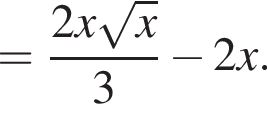
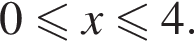 Значит, ее площадь равна
Значит, ее площадь равна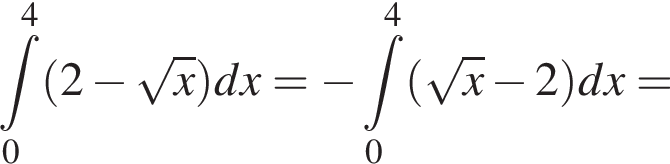
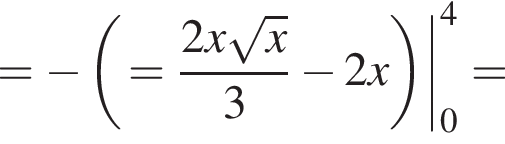
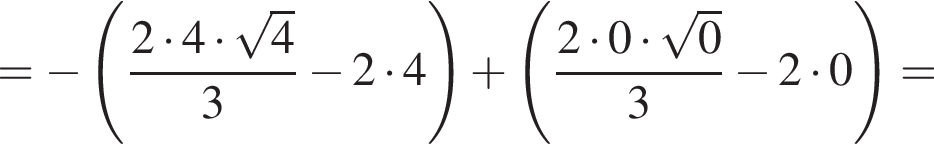
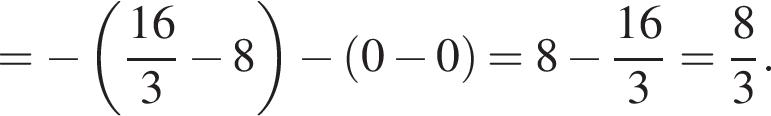
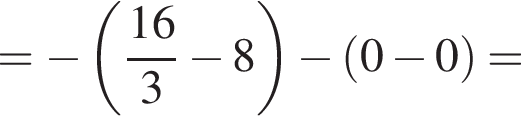
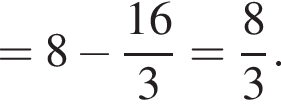
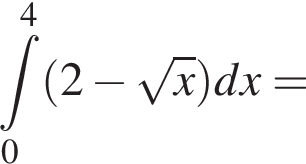
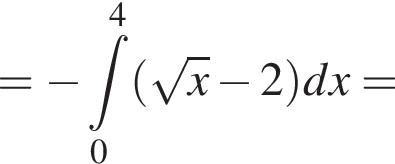
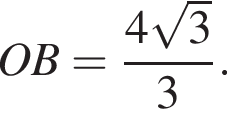 Выразим боковое ребро SB пирамиды из прямоугольного треугольника SOB, получим:
Выразим боковое ребро SB пирамиды из прямоугольного треугольника SOB, получим: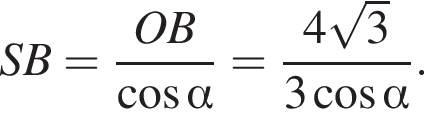
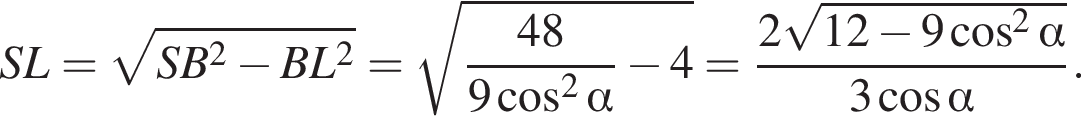
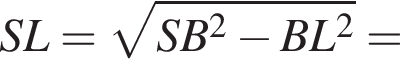
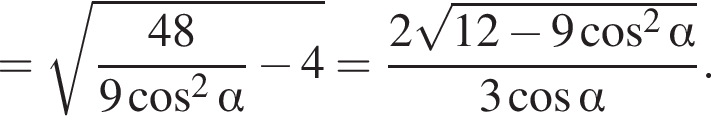
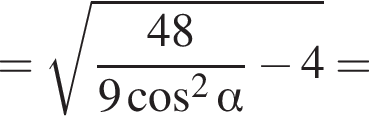
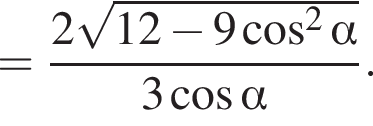
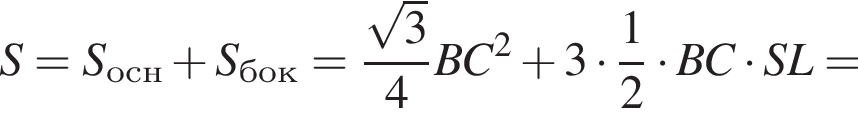
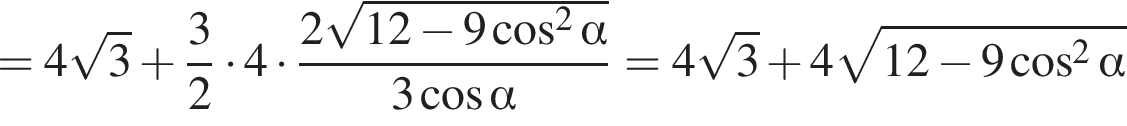
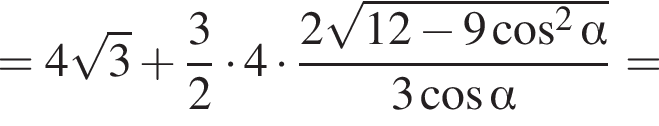
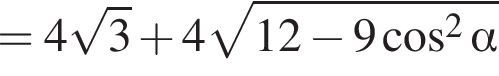
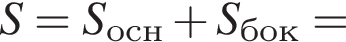
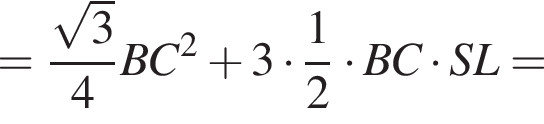
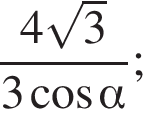 3)
3) 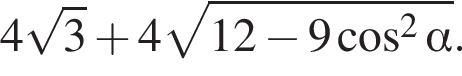
 то есть прямые AK и CK суть перпендикуляры к ребру двугранного угла между плоскостями SBA и SBC, а потому угол AKC — линейный угол двугранного угла при боковом ребре. Обозначим его δ.
то есть прямые AK и CK суть перпендикуляры к ребру двугранного угла между плоскостями SBA и SBC, а потому угол AKC — линейный угол двугранного угла при боковом ребре. Обозначим его δ.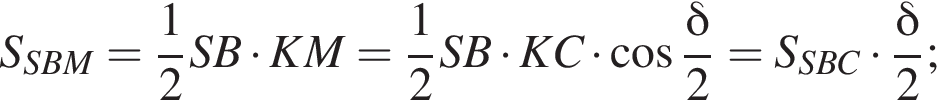
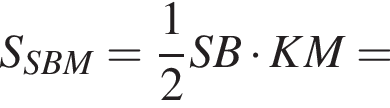
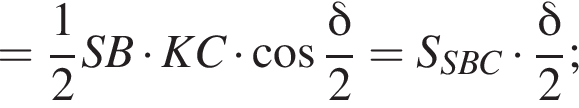
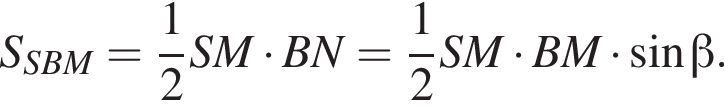
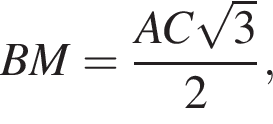 поэтому
поэтому 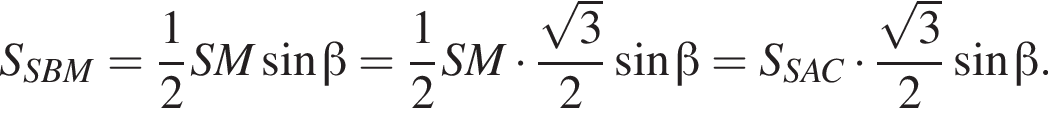
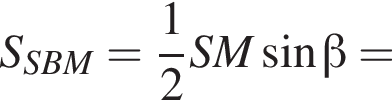
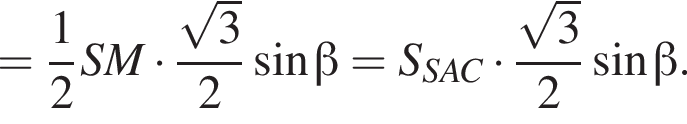
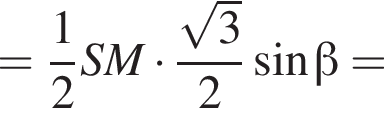
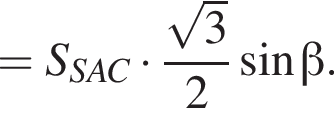
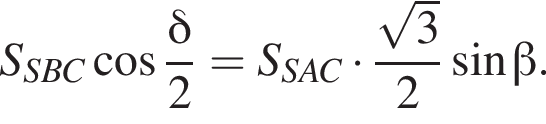
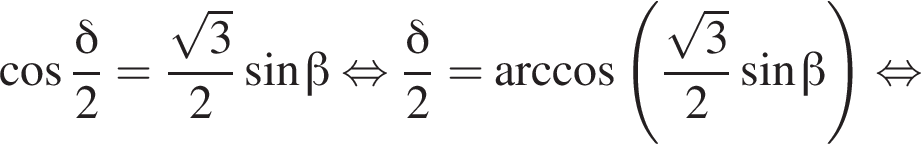
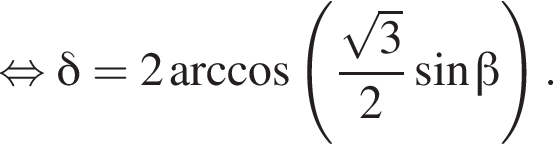
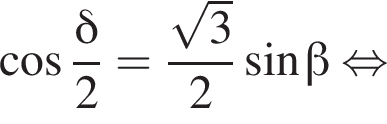
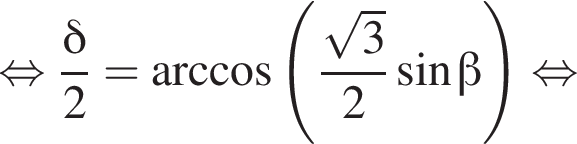
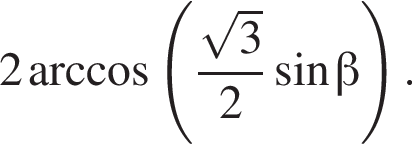

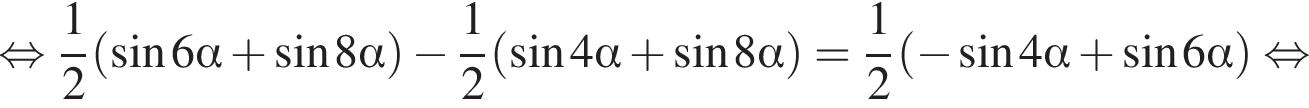
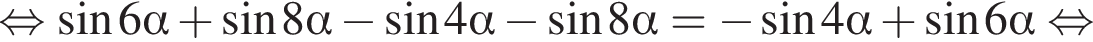

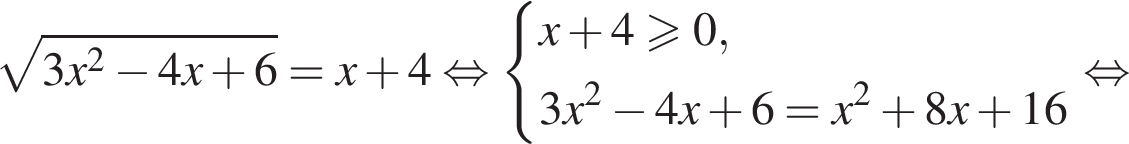
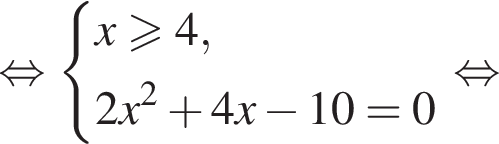
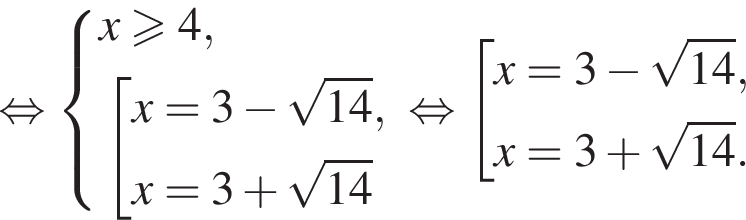
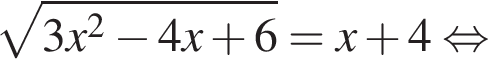
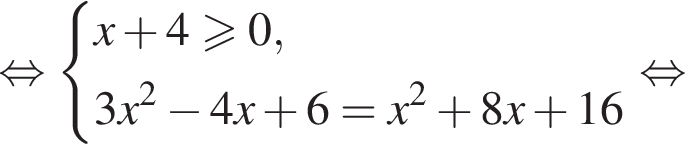
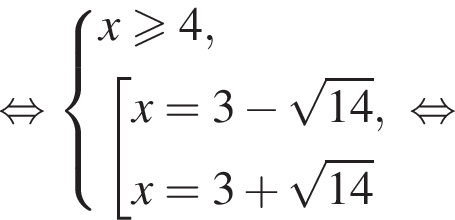
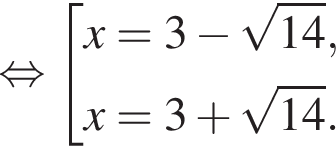

 Получаем
Получаем 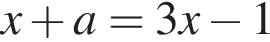 при условии
при условии  Получаем
Получаем 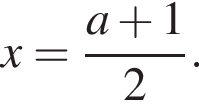 Условие принимает вид:
Условие принимает вид: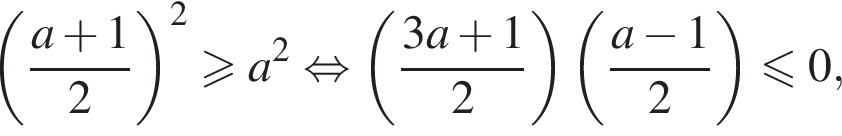
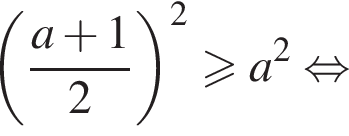
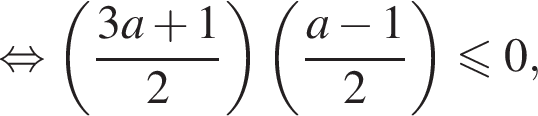
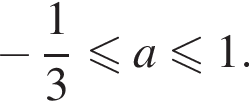 То есть в этом случае
То есть в этом случае 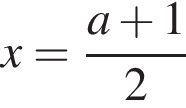 при
при 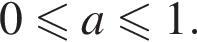
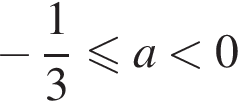 и
и