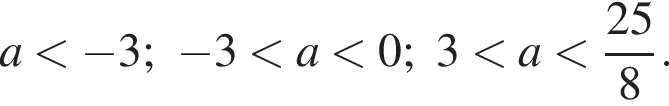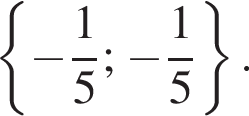Під час акції «Книги — дітям» школа отримала декілька книг, розподіл яких за рубриками показано на діаграмі: «І» — підручники та навчальні посібники, «ІІ» — методичні посібники, «ІІІ» — науково-популярна література, «ІV» - художня література (див. рис.). Яка кількість підручників та навчальних посібників надійшла до школи, якщо книг науково-популярної тематики та методичних посібників було 396?
Автомобіль проїхав деяку відстань, витративши 21 л палива. Витрата палива при цьому склала 9 л на 100 км пробігу. Потім автомобіль суттєво збільшив швидкість, внаслідок чого витрата палива зросла до 12 л на 100 км. Скільки літрів палива знадобиться автомобілю, щоб проїхати таку саму відстань?
З одиничного куба вирізана правильна чотирикутна призма зі стороною основи 0,5 і боковим ребром 1. Знайдіть площу поверхні частини куба, що залишилася.
Розв’яжіть рівняння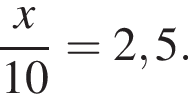 
На малюнку дві прямі перетинаються у точці О. Якщо
то кут BOC дорівнює:
Парна функція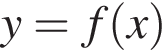 
визначена на проміжку 
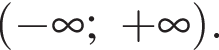Які з наведених тверджень є правильними?
I. 
II.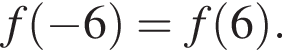 
III. Графік функції 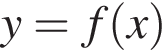симетричний відносно осі y.
Спростіть вираз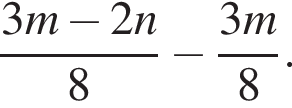 
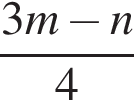
Закон Кулону можна записати у вигляді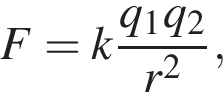
де F - сила взаємодії зарядів (у ньютонах),
і
— величини зарядів (у кулонах), k — коефіцієнт пропорційності (Нм 2 /Кл 2 ), а r — відстань між зарядами (в метрах). Використовуючи формулу, знайдіть величину заряду (у кулонах), якщо
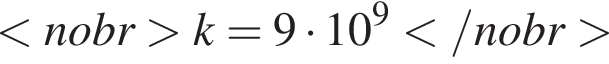
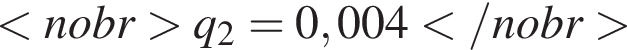
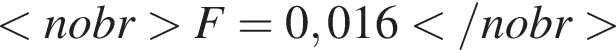
Спростіть вираз
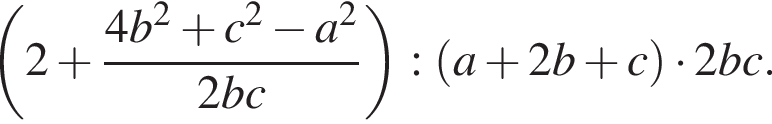
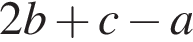
Які з наведених тверджень є правильними?
I. Якщо радіуси двох кіл дорівнюють 3 і 5, а відстань між їх центрами дорівнює 1, то ці кола перетинаються.
II. Вписані кути, що спираються на ту саму хорду кола, рівні.
III. Навколо будь-якого трикутника можна описати не більше одного кола.
Якому проміжку належить корінь рівняння 
Знайдіть похідну функції 
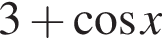
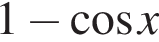
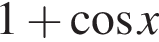
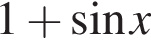
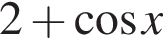
Розв’яжіть нерівність 
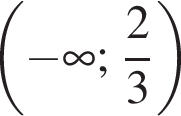
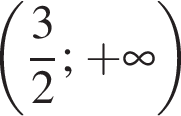
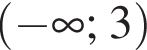
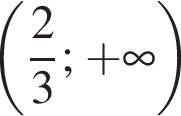
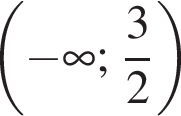
Обчисливши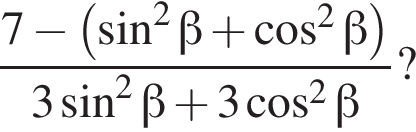 
У правильній трикутній піраміді SABC точка R – середина ребра BC, S – вершина. Відомо, що AB = 1, а SR = 2. Знайдіть площу бічної поверхні.
Каркас колеса огляду складається з двох однакових кіл, до яких прикріплено 18 кабінок на однаковій відстані одна від одної, та ребер (радіусів кіл), що з’єднують місця прикріплення кабінок та центри кіл (див. рисунок). Довжина кожного ребра дорівнює 27 м. Визначте довжину дуги AB кола із центром у точці О. Укажіть відповідь, найближчу до точної.
Товщиною каркасу знехтуйте. 3,2 м.
На рисунках (1−3) зображено графіки функцій, кожна з яких визначена на проміжку [−2; 2]. Установіть відповідність між графіком (1−3) функції та властивістю (А−Д) цієї функції.
А график функции проходит через точку (2; 1)
Б функция четная
В функция имеет две точки экстремума
Г график функции пересекает прямую у = 1 в одной точке
Д функция приобретает только отрицательные значения
Установіть відповідність між числовим виразом (1—4) та його значенням (А—Д).
1. 
2. 
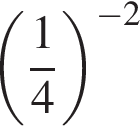
3. 
4. 
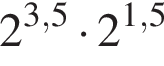
А 4
Б 8
В 16
Г 32
Д 64
У довільному трикутнику ABC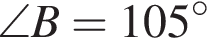 
та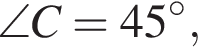
а довжина сторони AB дорівнює 12.
Встановіть відповідність між відрізками (1-3) і їх довжинами (А−Д).
1 AC
2 висота трикутника АВС, проведена до сторони AC
3 радіус кола, описаної навколо трикутника АВC
А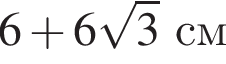 
Б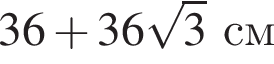 
В 
Г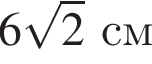 
Д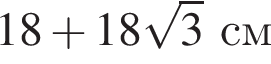 
Циліндр і конус мають рівні об’єми та рівні радіуси основ. Площа основи циліндра дорівнює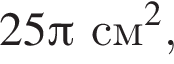 
а його об’єм — 
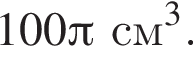До кожного початку речення (1—4) доберіть його закінчення (А—Д) так, щоб утворилося правильне твердження.
1. Висота циліндра дорівнює
2. Висота конуса дорівнює
3. Радіус основи циліндра дорівнює
4. Твірна конуса дорівнює
А 4 см
Б 5 см
В 8 см
Г 12 см
Д 13 см
Для приготування чайної суміші змішали індійськи й та цейлонський чай у віднош енні 10 : 13, причом у індійського чаю в зял
1. Скільки грамів чайної суміші отримали?
2. На скільки відсотків у суміші цейлонського чаю більше, ніж індійського?
У довільній трапеції ABCD середня лінія MN дорівнює 10 см, а відрізок LK, що з'єднує середини діагоналей, дорівнює 3 см. Висота трапеції ABCD дорівнює 6 см.
1. Вычислить отрезок AD.
2. Вычислить высоту трапеции AMND.
В прямоугольной системе координат в плоскости заданы векторы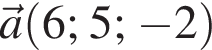 
и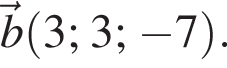 
1. Укажите координаты вектора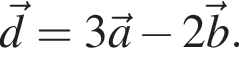 
В ответе запишите их сумму.
2. Найти модуль вектора 
У геометричній прогресії
відомо що 
.
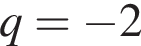1. Знайти п’ятий член цієї прогресії.
2. Найдите суммы первых пяти членов этой прогрессии
Платіжний термінал протягом робочого дня може вийти з ладу. Ймовірність цієї події 0,07. У торговому центрі незалежно один від одного працюють два такі платіжні термінали. Знайдіть ймовірність того, що хоча б один із них протягом робочого дня буде справний.
Човен проплив 18 км проти течії річки, витративши вдвічі менше часу, ніж на подолання 48 км за течією. Власна швидкість човна є сталою. Визначте власну швидкість човна (у км/год), якщо швидкість течії дорівнює 2,5 км/год.
Спростіть вираз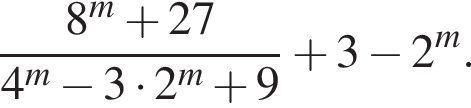
Розв'яжіть нерівність
У відповіді запишіть суму всіх його рішень на проміжку [0; 12].
У магазині в продажу є 6 видів тарілок, 8 видів блюдець та 12 видів чашок. Олена збирається купити бабусі в подарунок у цьому магазині або чашку та блюдце, або лише тарілку. Скільки всього є способів в Олени купити бабусі такий подарунок?
| x | y |
|---|---|
| −3 | |
| 0 | |
| 3 |
Задано функцію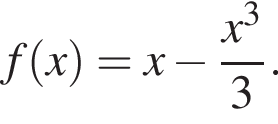
1. Для наведених у таблиці значень аргументів х визначте відповідні їм значення у (див. таблицю).
2. Знайдіть координати точок перетину графіка функції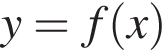
з осями координат.
3. Знайдіть похідну f' функції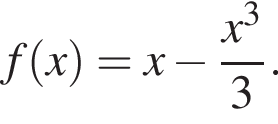
4. Визначте нулі функції f' .
5. Визначте проміжки зростання та спадання, точки екстремуму функції f .
6. Побудуйте ескіз графіка функції f .
Бічні ребра правильної трикутної піраміди дорівнюють 6. Плоский кут при вершині дорівнює γ.
1. Зобразіть на малюнку цю піраміду та кут γ.
2. Знайдіть висоту піраміди.
3. Знайдіть об'єм піраміди.
Відповідно до умови завдання 31 (№ 3494) сторона основи правильної трикутної піраміди дорівнює 6. Плоский кут при вершині дорівнює γ.
а) Зобразіть на малюнку цю піраміду та побудуйте лінійний кут двогранного кута при бічному ребрі.
б) Знайдіть цей кут.
Доведіть тотожність: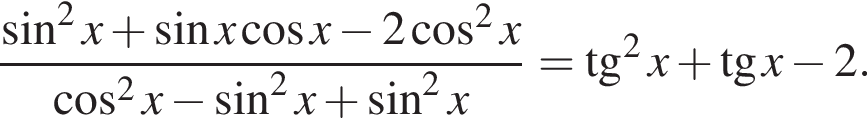
Задано систему рівнянь
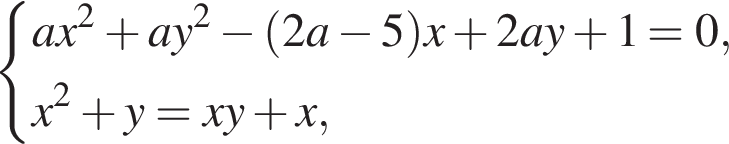
1. Вирішіть цю систему, якщо
2. Знайдіть усі значення а , при кожному з яких система рівнянь має рівно чотири різні розв'язки.
автомобиль израсходовал 21 л, тогда при расходе топлива 
автомобиль израсходует: 
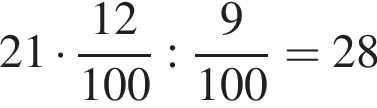л.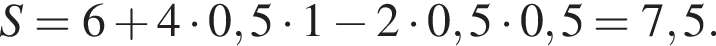
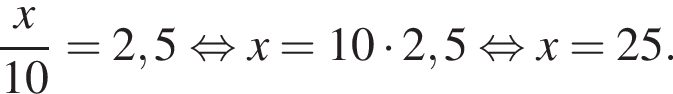
равна 360°, поэтому 
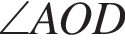равен 60°. Углы 
и 
и 
— вертикальные, следовательно, 
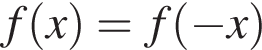при всех x, поэтому верными являются второе и третье утверждения.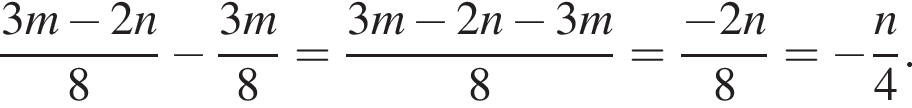
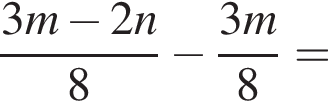
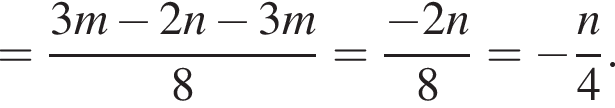
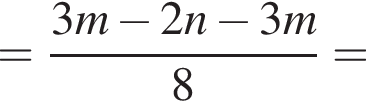
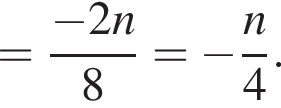
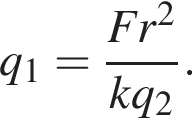
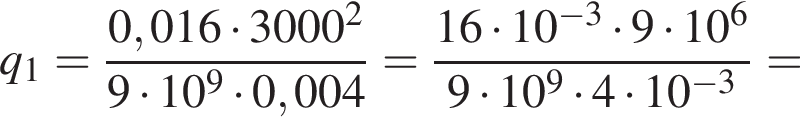
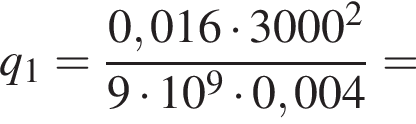
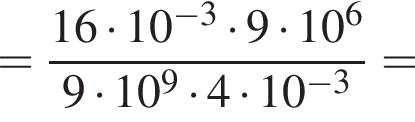
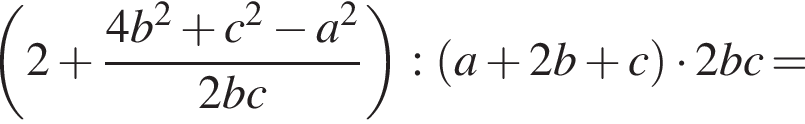
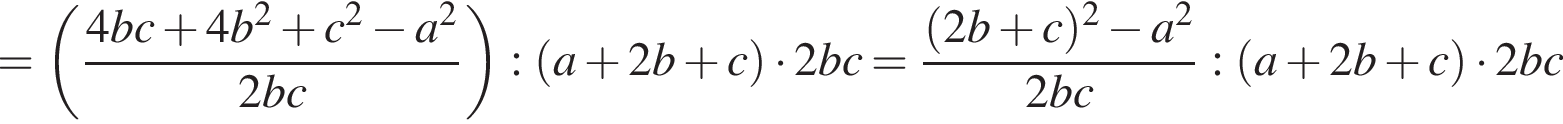
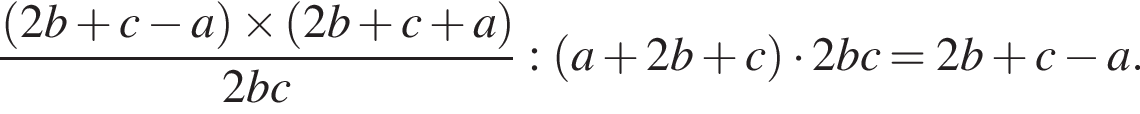
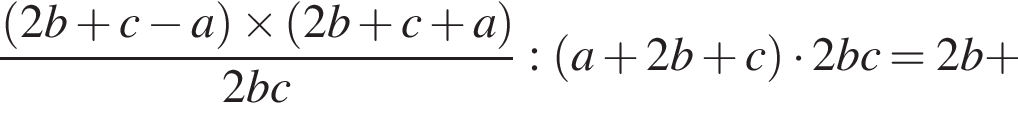
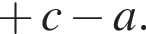
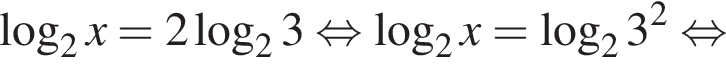
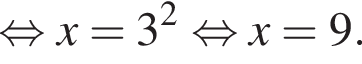
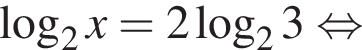
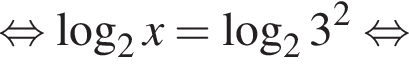
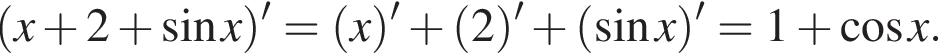
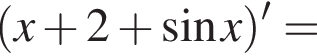
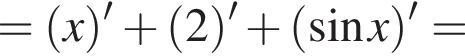
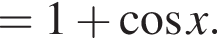
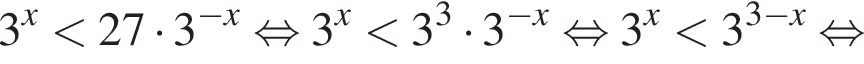
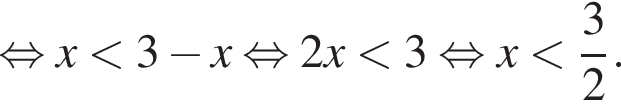
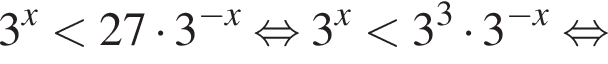
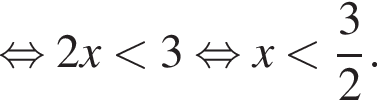
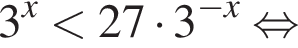
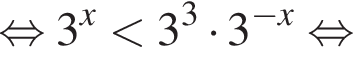
из закона Кулона:
поэтому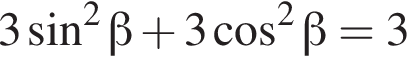 
и выражение из условия равно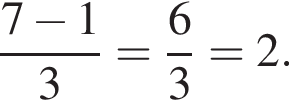 
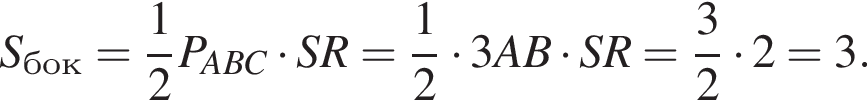
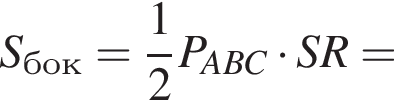
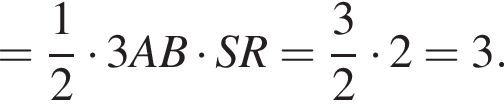
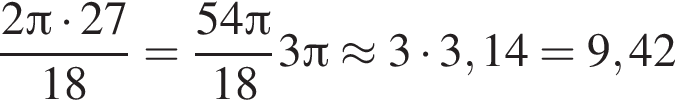м
м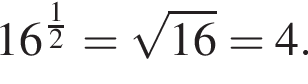
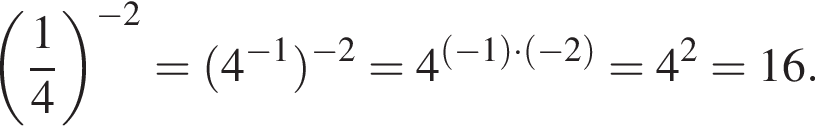
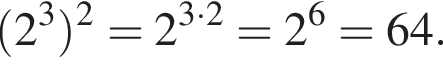
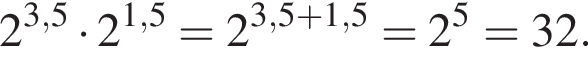
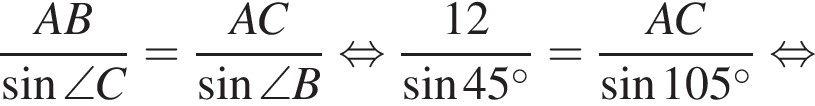
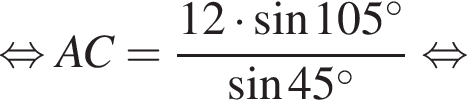
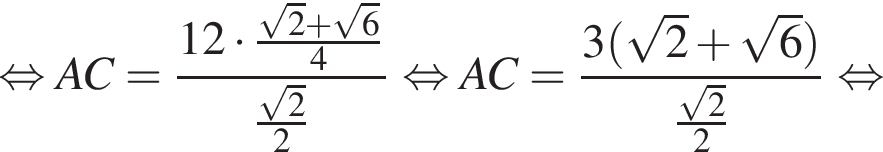
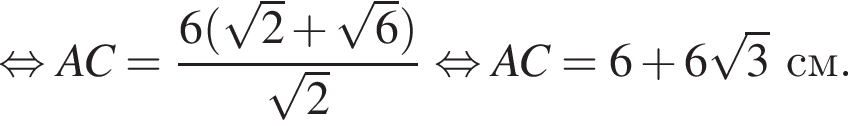
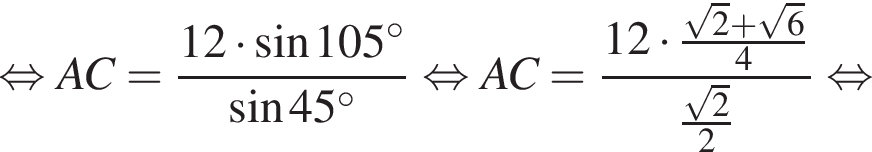
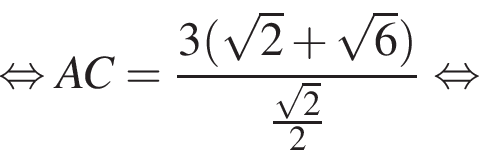
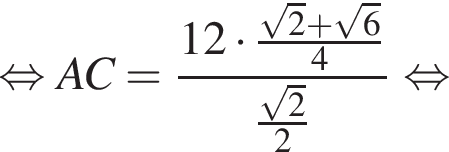
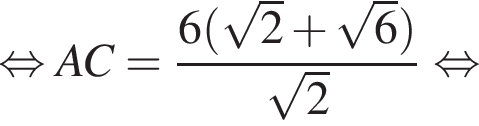
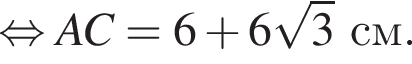
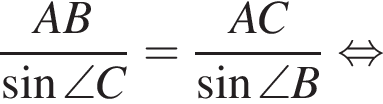
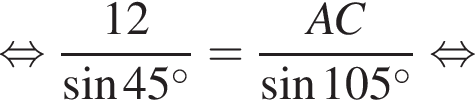
Проведем в треугольнике ABC высоту BH. Треугольник ABH — прямоугольный, катет BH лежит напротив угла, равного 30°, а значит,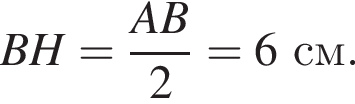 
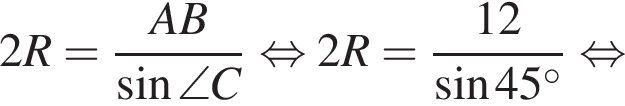
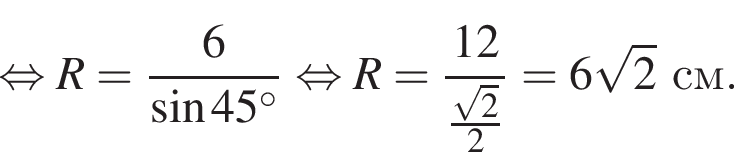
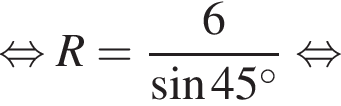
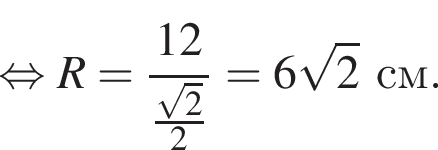
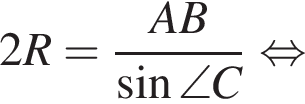
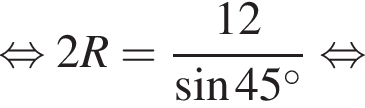
отсюда 
Тогда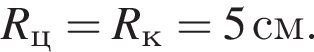 
Итак, 3 — B.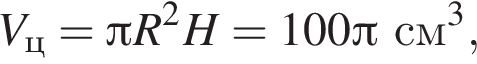
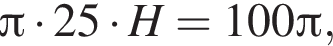отсюда 
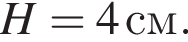Высота цилиндра равна 4 см, получаем: 1 — А.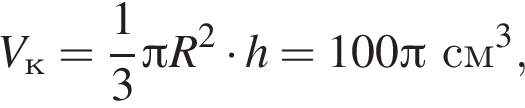
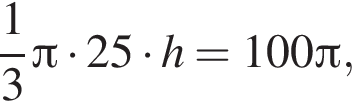отсюда 
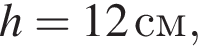следовательно, 2 — Г. 
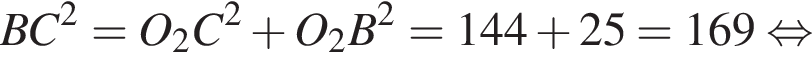
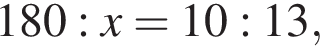откуда по правилу пропорции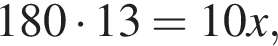 
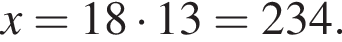Значит всего в смеси 
грамм чая. Цейлонского чая больше чем индийского в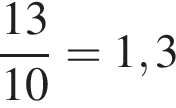 
раза, то есть на 
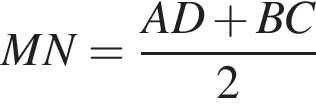и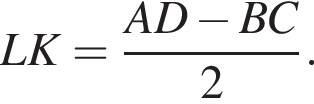 
Составим и решим систему уравнений: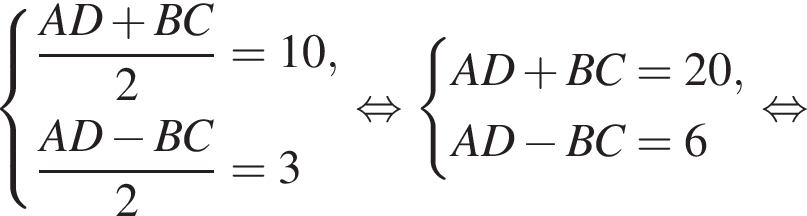
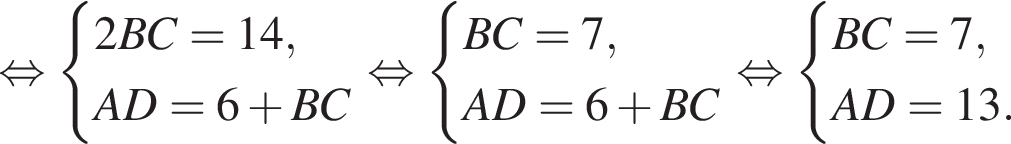
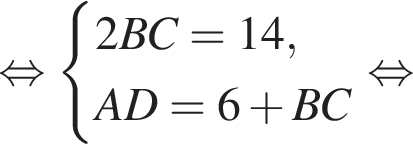
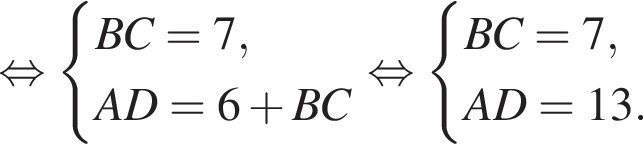
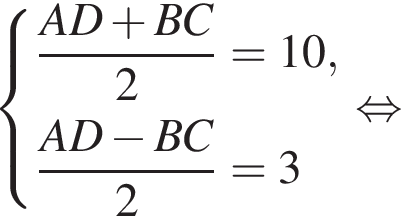
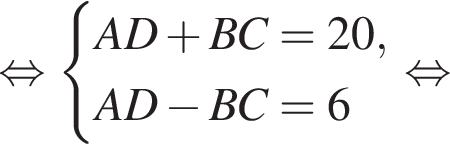
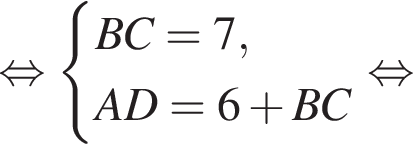
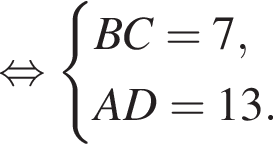
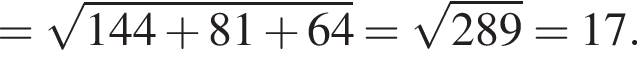
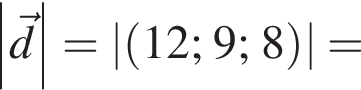
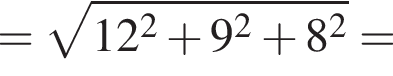
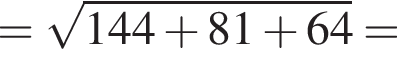
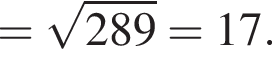
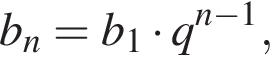имеем: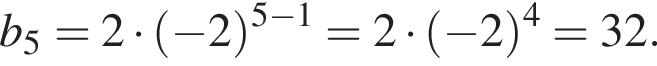
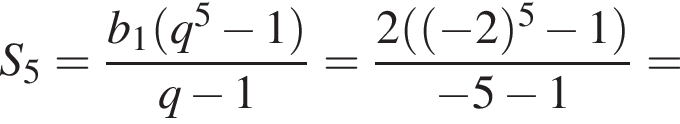
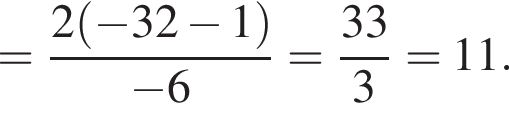
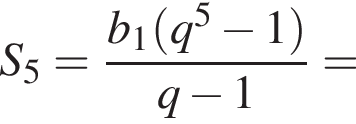
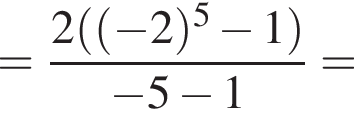
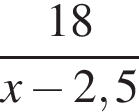ч. Тогда время, затраченное на 18 километров против течения, равно 
часов, а на 48 километров по течению — 
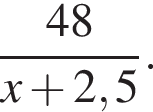По условию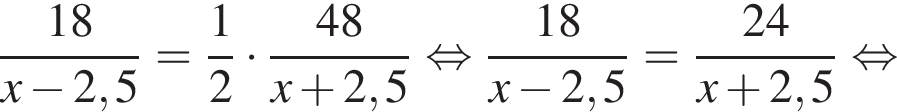
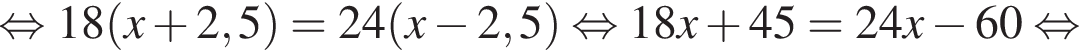
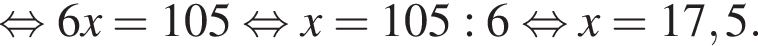
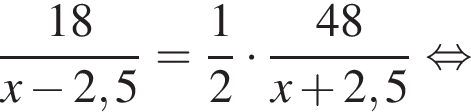
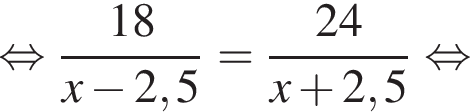
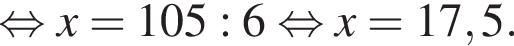
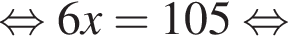
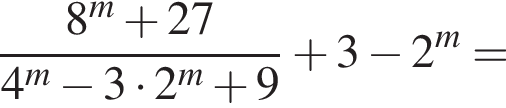
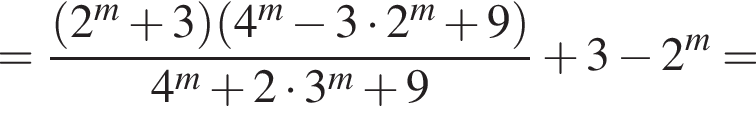
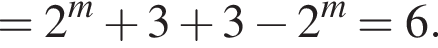
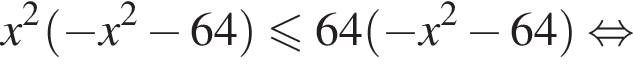
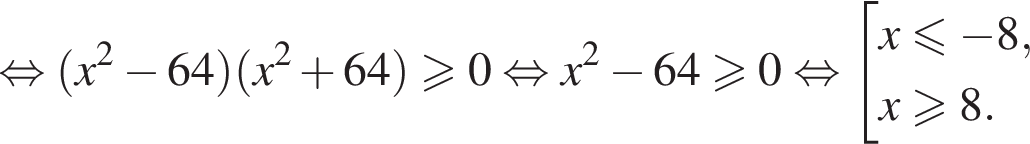
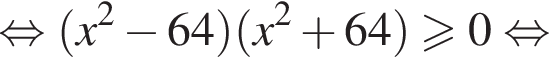
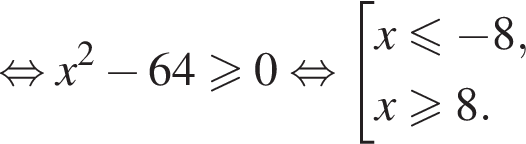
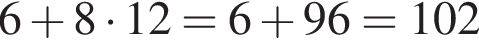вариантов выбора чашки и блюдца (независимо друг от друга). Значит, всего есть 
варианта.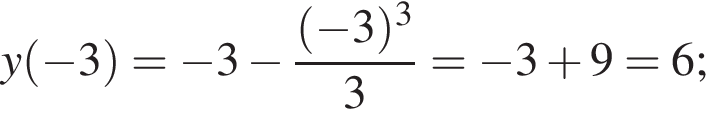
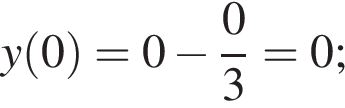
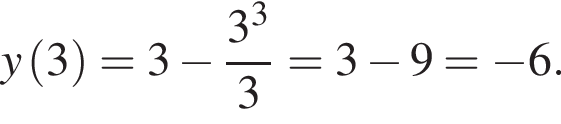
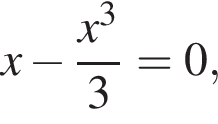откуда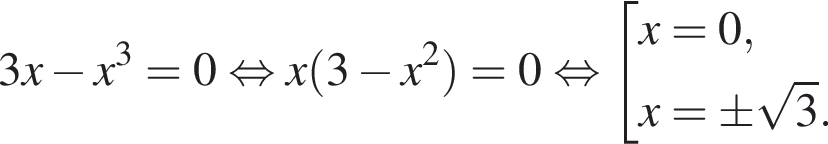 
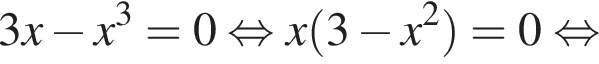
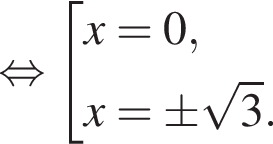
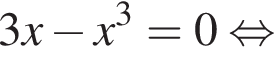
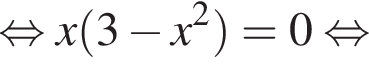
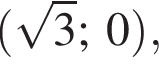
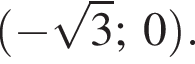Первая заодно будет точкой пересечения с осью ординат.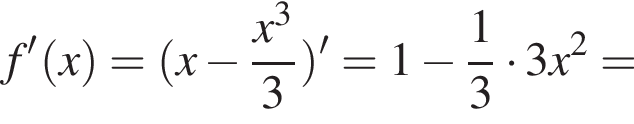
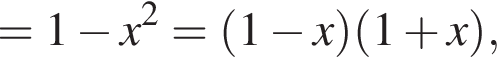
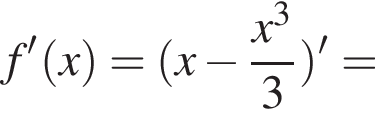
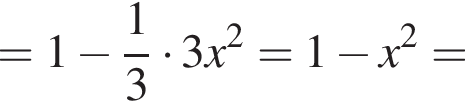
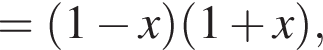
и отрицательно при 
или 
убывает при 
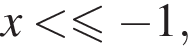возрастает при 
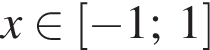и убывает при 
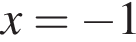— точка минимума, а точка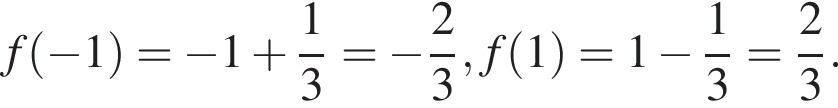 
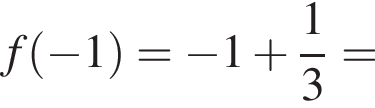
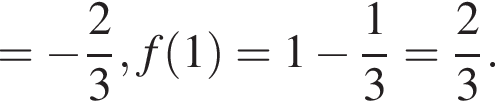
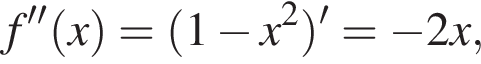— точка максимума функции,
что отрицательно при 
и положительно при 
Значит, функция выпукла вверх при 
будет точкой перегиба, 
Функция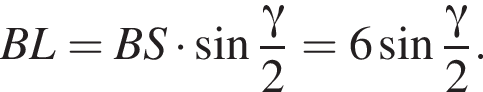 
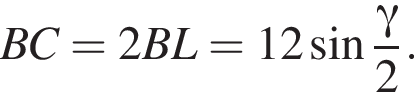Найдём площадь равностороннего треугольника, лежащего в основании: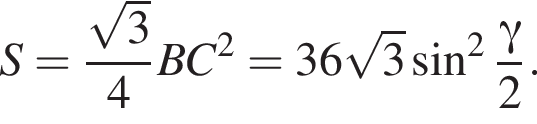
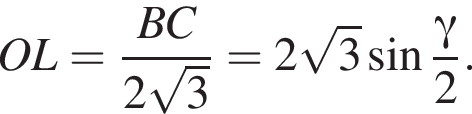Апофема треугольника BSC равна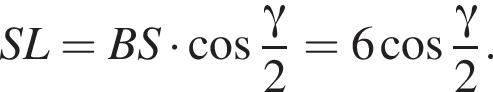 
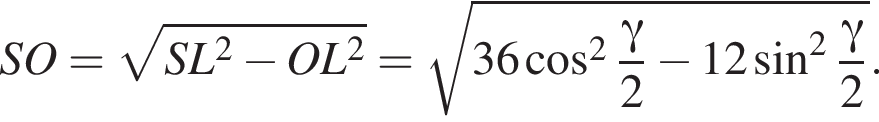
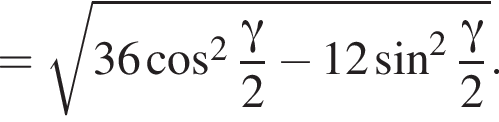
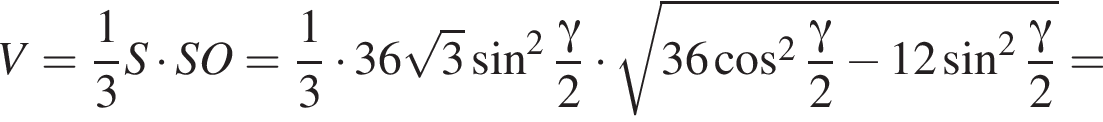
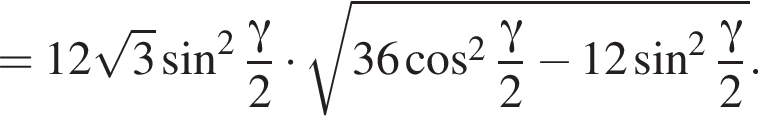
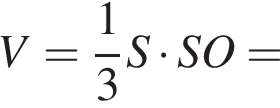
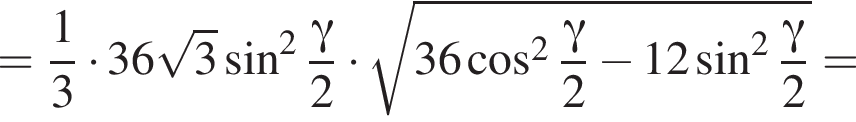
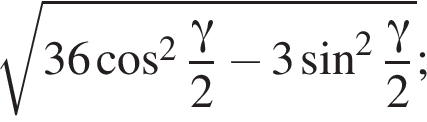3) 
то есть прямые AK и CK суть перпендикуляры к ребру двугранного угла между плоскостями SBA и SBC, а потому угол AKC — линейный угол двугранного угла при боковом ребре. Обозначим его δ.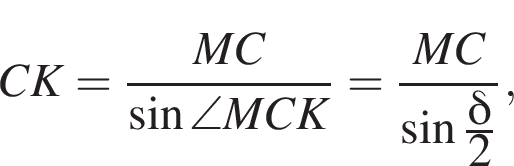
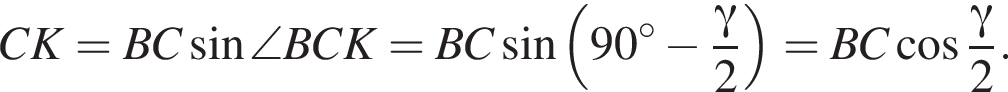
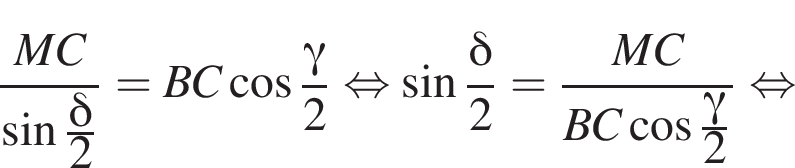
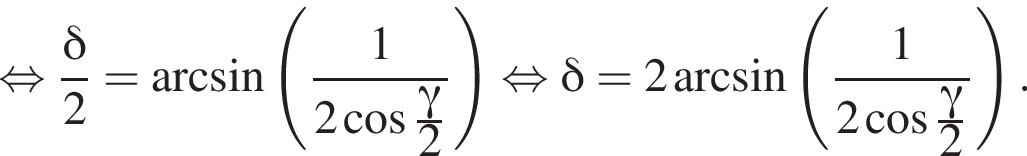
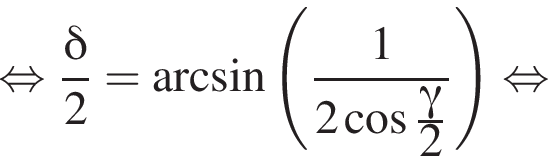
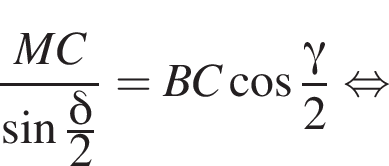
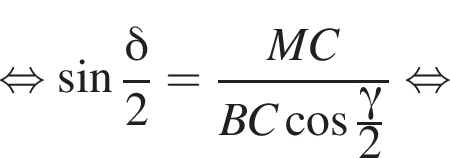
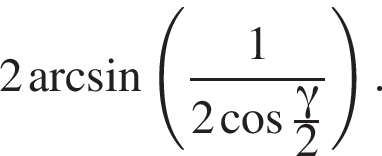
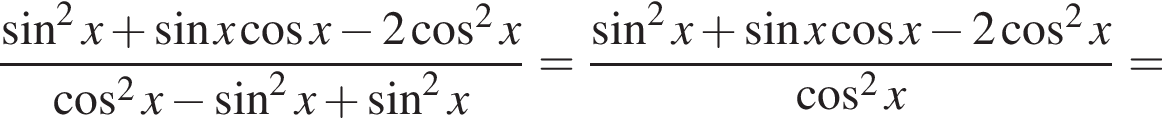
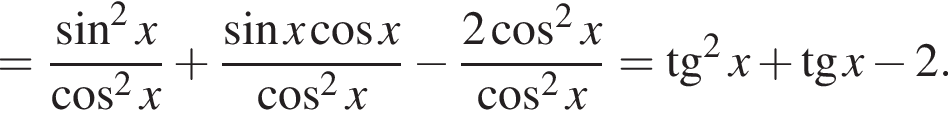
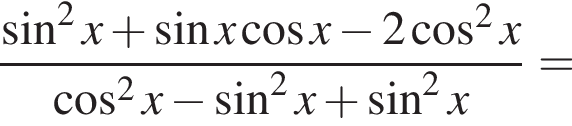
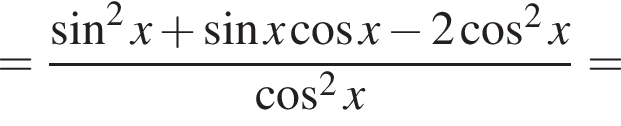
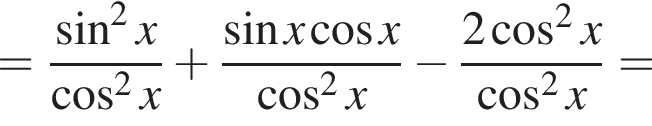
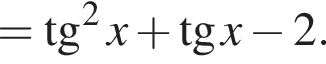
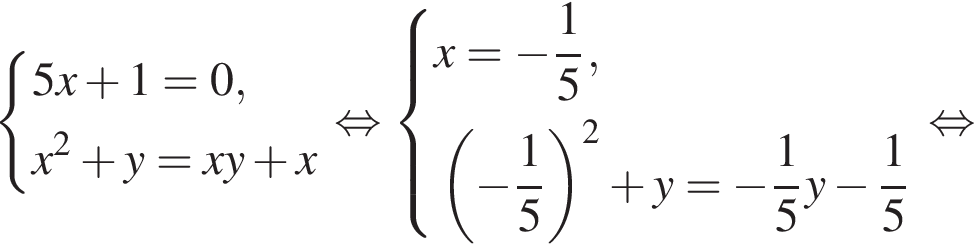
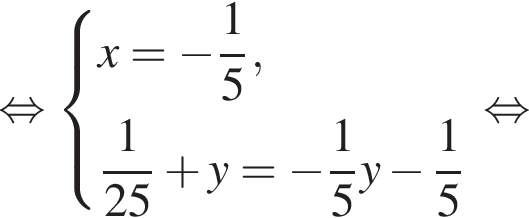
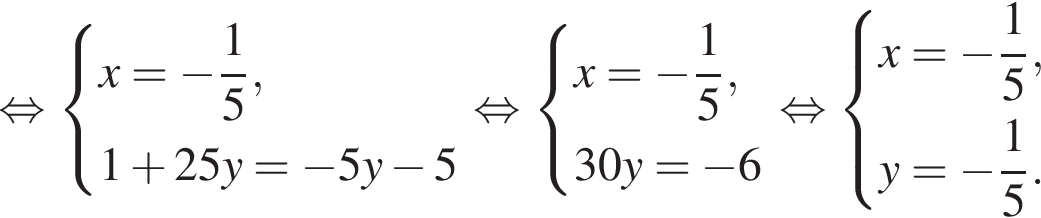
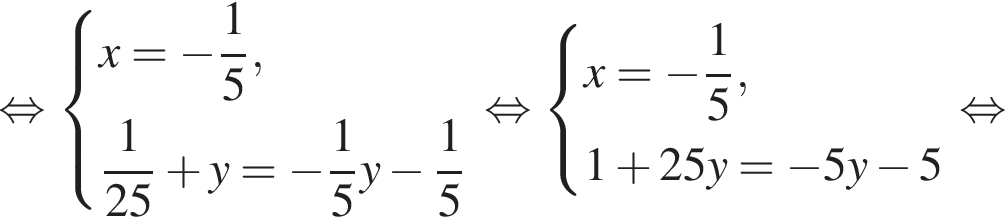
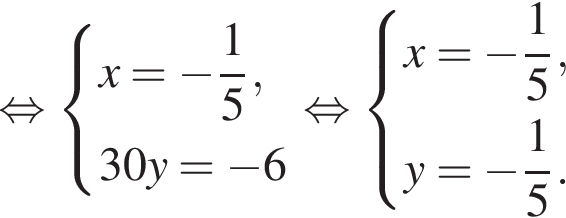
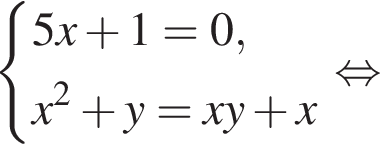
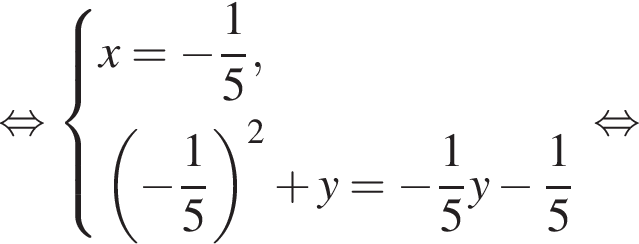
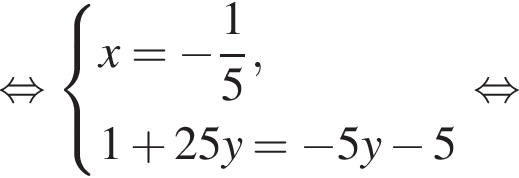
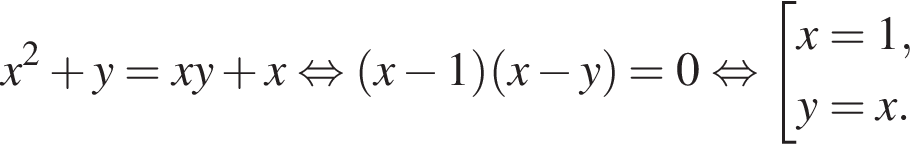
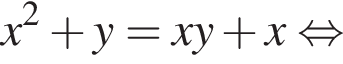
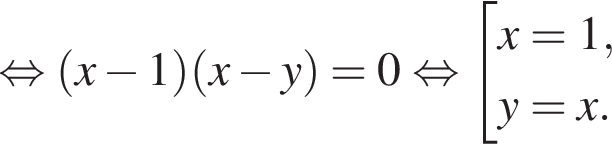
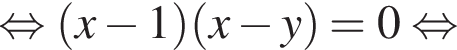
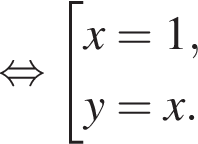
при подстановке в первое уравнение системы 
получаются квадратные уравнения. Значит, исходная система уравнений имеет ровно 4 различных решения тогда и только тогда, когда каждое из этих уравнений имеет ровно два корня и пара чисел (1;1) не является решением исходной системы.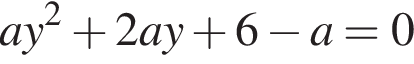
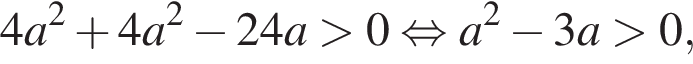
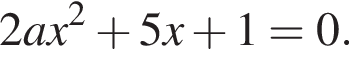
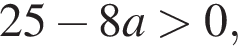
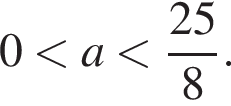
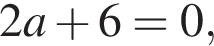получаем:
получаем 
или 
то есть a = −3.
