1. Тип 7 № 1021 

Классификатор алгебры: 1\.5\. Преобразования буквенных выражений со степенями и корнями
Перетворення виразів. Прості перетворення
i
Спростіть вираз 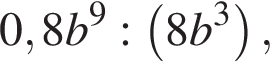 де
де ![]()
А) 0,1b6
Б) 10b6
В) 6,4b12
Г) 0,1b3
Д) 10b3
Решение. Упростим: 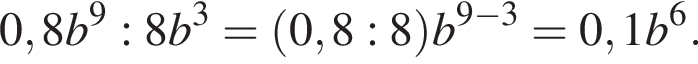
Правильный ответ указан под номером 1.
Ответ: 1
1021
1
Классификатор алгебры: 1\.5\. Преобразования буквенных выражений со степенями и корнями
 см.
см.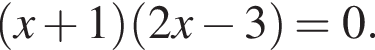
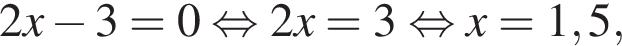 либо
либо 
 то d дорівнює?
то d дорівнює?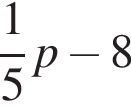

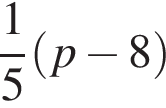

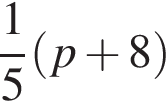
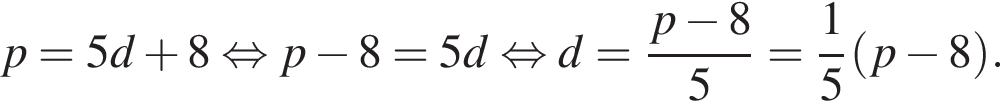

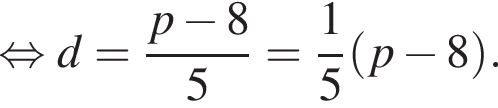
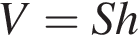
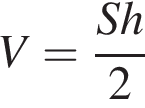

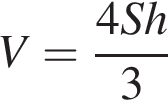
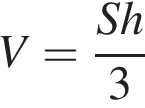
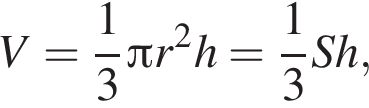
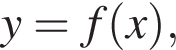 визначеної на проміжку [1; 8]. Скільки нулів мае ця функція на заданому проміжку?
визначеної на проміжку [1; 8]. Скільки нулів мае ця функція на заданому проміжку?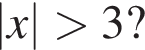
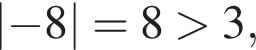 последнее число подходит. Остальные не подходят, это легко проверить.
последнее число подходит. Остальные не подходят, это легко проверить.
 при всех x, первое — верно (только не неотъемлемые, а неотрицательные значения). Она возрастает на всей области определения
при всех x, первое — верно (только не неотъемлемые, а неотрицательные значения). Она возрастает на всей области определения 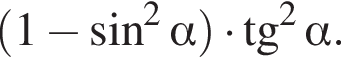
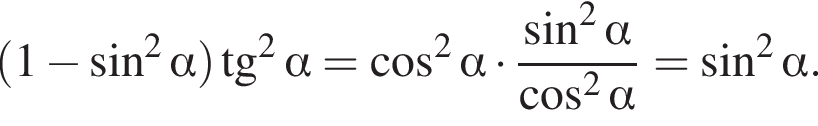
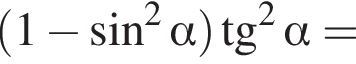
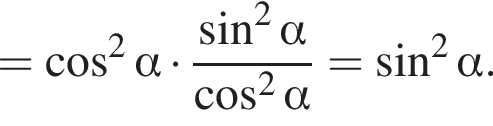
 человек.
человек.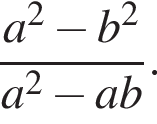
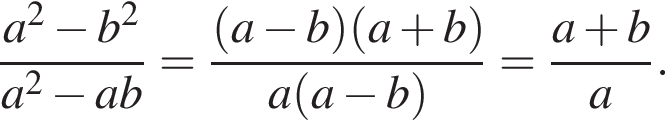


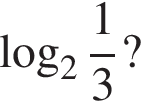

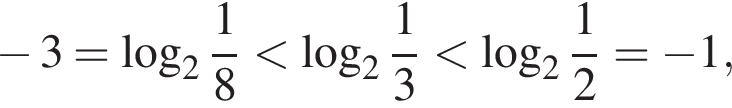
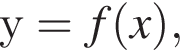 визначеної на проміжку [−3; 3]. Одна з наведених точок належить графіку функції
визначеної на проміжку [−3; 3]. Одна з наведених точок належить графіку функції  Укажіть цю точку.
Укажіть цю точку. отличается от
отличается от 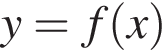 симметрией относительно горизонтальной оси. Поэтому можно рассмотреть точки, симметричные данным, и изучить, какая из них попадет на график
симметрией относительно горизонтальной оси. Поэтому можно рассмотреть точки, симметричные данным, и изучить, какая из них попадет на график 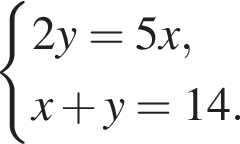
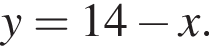 Подставляя в первое уравнение, получаем
Подставляя в первое уравнение, получаем 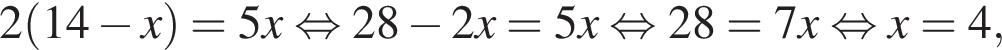

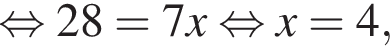
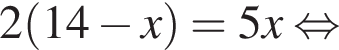

 и
и 



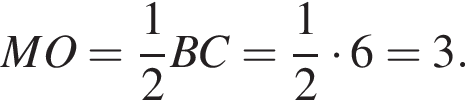 Значит,
Значит, 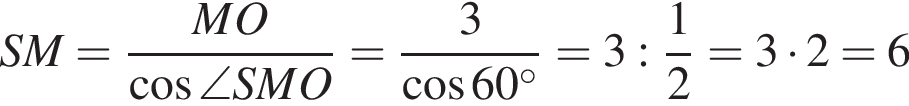
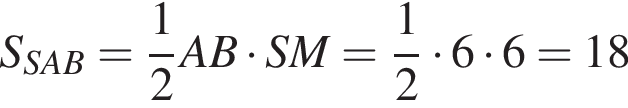 см2.
см2. см2.
см2.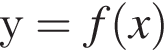 і
і 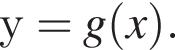 Укажіть формулу для обчислення площі зафарбованої фігури.
Укажіть формулу для обчислення площі зафарбованої фігури.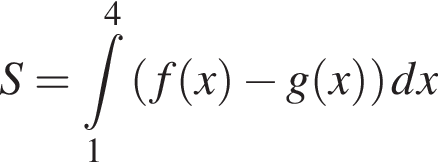
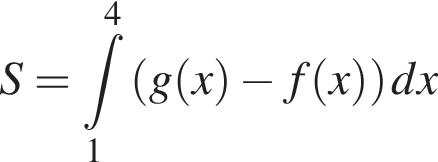
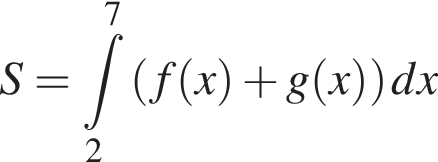
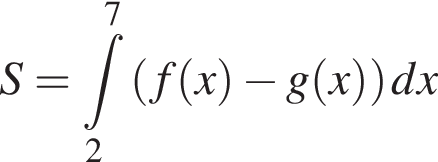
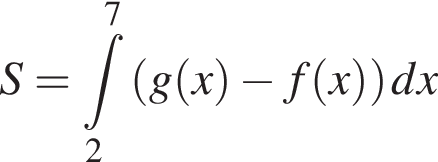
 м,
м, м
м м.
м.
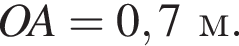 Мысленно продолжим AD и ME до пересечения в точке T, тогда OATM окажется квадратом. Тогда
Мысленно продолжим AD и ME до пересечения в точке T, тогда OATM окажется квадратом. Тогда 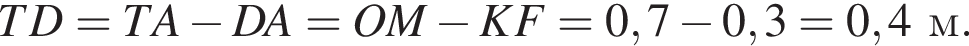
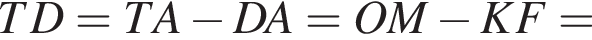
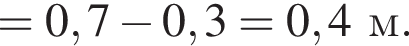
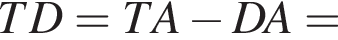

 м.
м.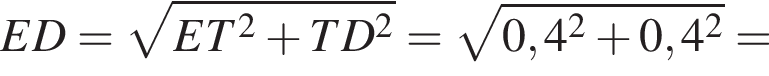
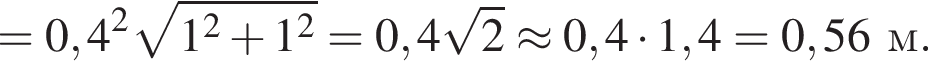

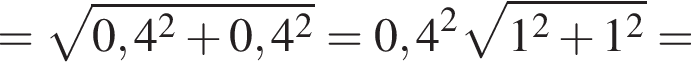
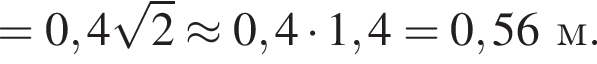
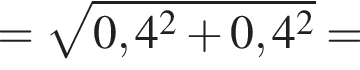
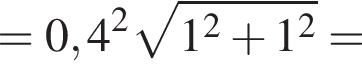
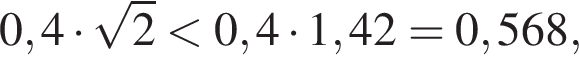 поэтому ошибка при вычислении не была достаточно существенной, чтобы на самом деле правильным ответом было 0,6.
поэтому ошибка при вычислении не была достаточно существенной, чтобы на самом деле правильным ответом было 0,6.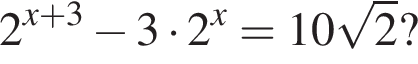
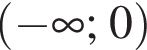

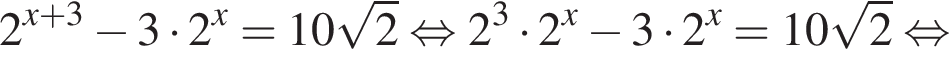

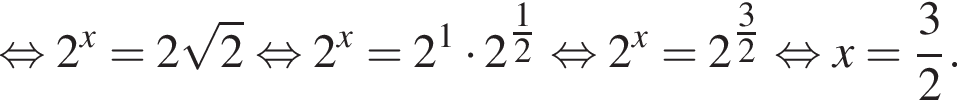
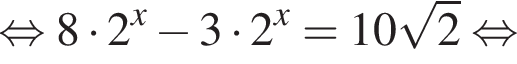
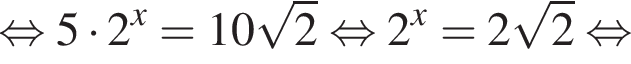
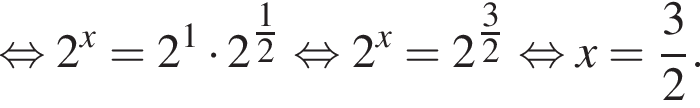
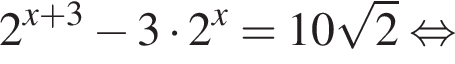
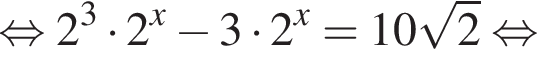
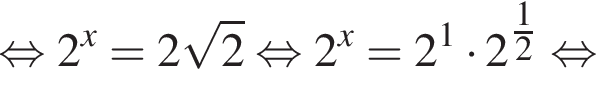
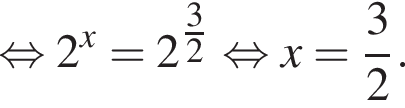

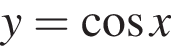
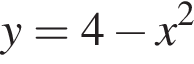
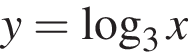
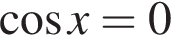 имеет бесконечно много решений, поэтому второй график имеет бесконечно много точек пересечения. Функция
имеет бесконечно много решений, поэтому второй график имеет бесконечно много точек пересечения. Функция 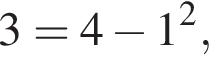 а в остальные уравнения эта точка не подходит. Функция
а в остальные уравнения эта точка не подходит. Функция 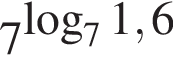
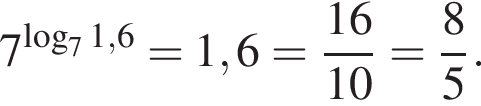
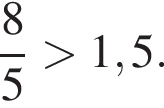 Первая и третья дроби даже больше 2, а вторая меньше единицы. Действительно,
Первая и третья дроби даже больше 2, а вторая меньше единицы. Действительно, 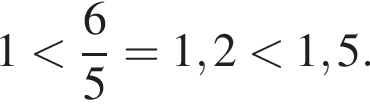
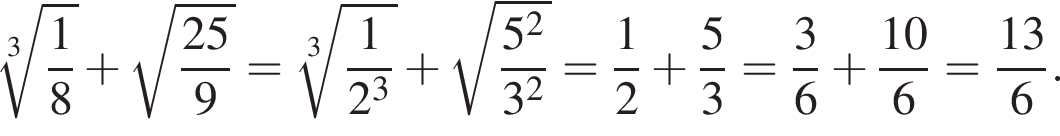
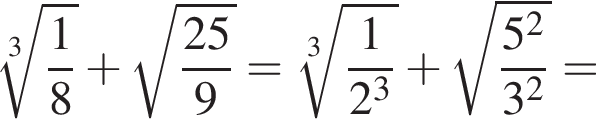
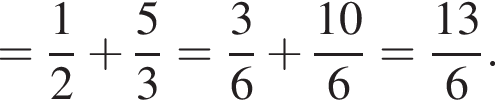
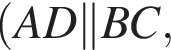
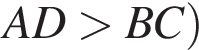 з більшою бічною стороною
з більшою бічною стороною 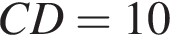 описано навколо кола радіуса 4. Установіть відповідність між величиною (1−4) та її числовим значенням (А−Д).
описано навколо кола радіуса 4. Установіть відповідність між величиною (1−4) та її числовим значенням (А−Д).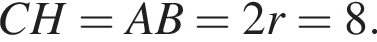 Из прямоугольного треугольника CHD получаем
Из прямоугольного треугольника CHD получаем 
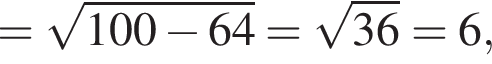

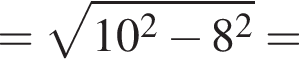
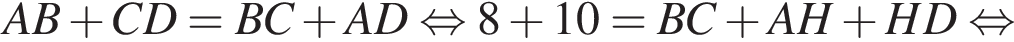

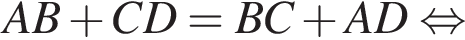


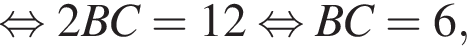
 В таком случае, средняя линия трапеции равна
В таком случае, средняя линия трапеции равна 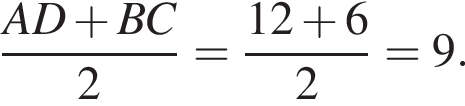
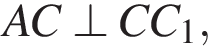 потому что
потому что 
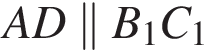 как ребра параллелепипеда и
как ребра параллелепипеда и  Значит, AB1C1D — параллелограмм, поэтому
Значит, AB1C1D — параллелограмм, поэтому 
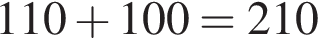 или
или 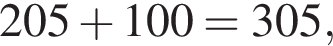 в зависимости от того, какие именно грузы объединить.
в зависимости от того, какие именно грузы объединить.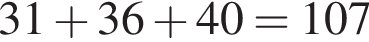 кг
кг От 300 это составит
От 300 это составит 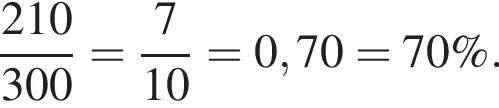
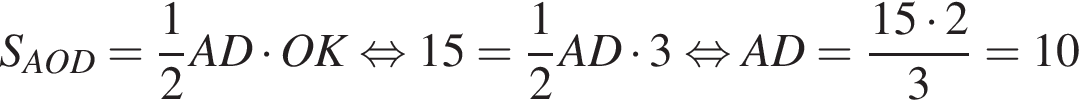
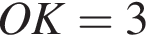 см
см см
см см
см
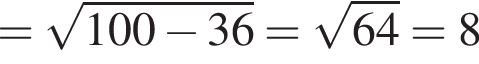
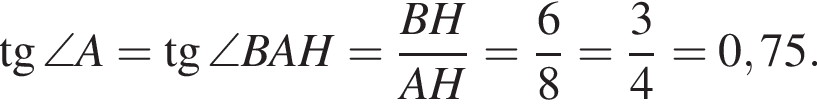

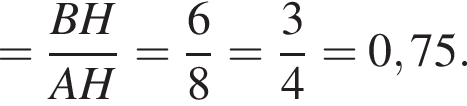
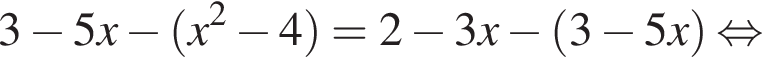


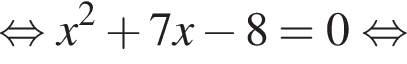
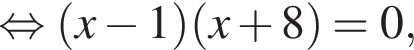
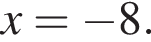 По условию надо выбрать отрицательное x.
По условию надо выбрать отрицательное x.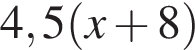 км. По условию эти расстояния равны, откуда
км. По условию эти расстояния равны, откуда 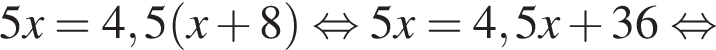

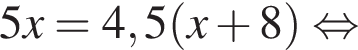
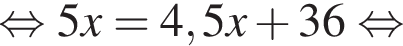
 способами. Совмещая каждый способ из первого набора с каждым способом из второго, получим
способами. Совмещая каждый способ из первого набора с каждым способом из второго, получим 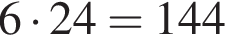 способа.
способа.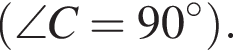 Коло з центром у точці A, задане рівнянням
Коло з центром у точці A, задане рівнянням 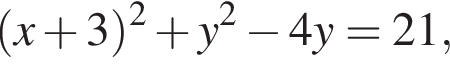 проходить через вершину C. Сторона AC паралельна осі y, довжина сторони BC втричі більша за довжину сторони AC. Визначте координати вершини B (xв; yв), якщо вона лежить у першій координатній чверті. У відповідь запишіть суму xв + yв.
проходить через вершину C. Сторона AC паралельна осі y, довжина сторони BC втричі більша за довжину сторони AC. Визначте координати вершини B (xв; yв), якщо вона лежить у першій координатній чверті. У відповідь запишіть суму xв + yв.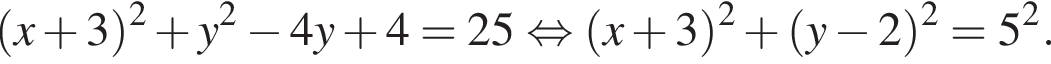
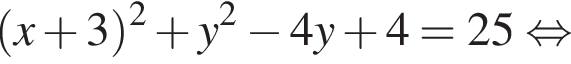
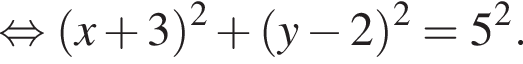
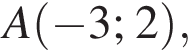 а радиус ее 5. Поскольку прямая AC горизонтальна, координаты точки C отличаются от координат точки A только абсциссой, причем на радиус окружности. Значит, либо
а радиус ее 5. Поскольку прямая AC горизонтальна, координаты точки C отличаются от координат точки A только абсциссой, причем на радиус окружности. Значит, либо 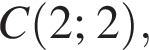 либо
либо 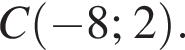 Далее, угол C прямой, поэтому BC — вертикальный отрезок длиной
Далее, угол C прямой, поэтому BC — вертикальный отрезок длиной 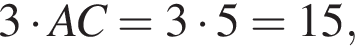 значит координаты точки B отличаются от координат точки C только ординатой, на 15 в какую-то сторону. По условию точка B лежит в первой четверти, то есть обе ее координаты положительны. Значит во-первых, у C не могут быть координаты
значит координаты точки B отличаются от координат точки C только ординатой, на 15 в какую-то сторону. По условию точка B лежит в первой четверти, то есть обе ее координаты положительны. Значит во-первых, у C не могут быть координаты 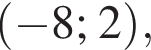 а во-вторых, из точек
а во-вторых, из точек 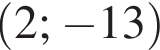 на роль B надо выбирать первую. Тогда
на роль B надо выбирать первую. Тогда 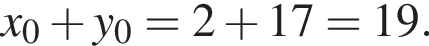
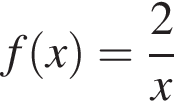 i
i 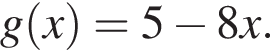
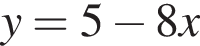 — прямая, проходящая через точки
— прямая, проходящая через точки 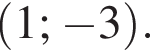 Они изображены на рисунке.
Они изображены на рисунке.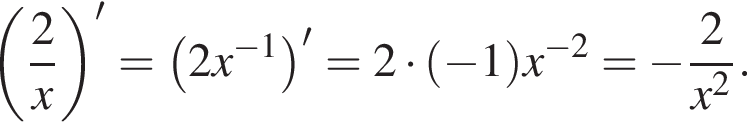
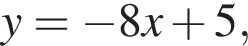 если их коэффициенты при x в уравнении будут равны −8. Угловой коэффициент касательной равен значению производной в точке касания, остается решить уравнение
если их коэффициенты при x в уравнении будут равны −8. Угловой коэффициент касательной равен значению производной в точке касания, остается решить уравнение 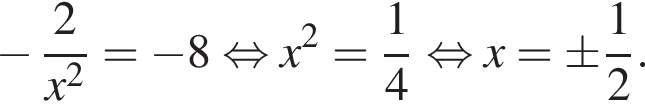
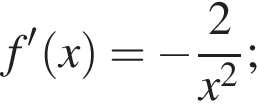 4)
4) 
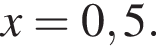
 від неї.
від неї.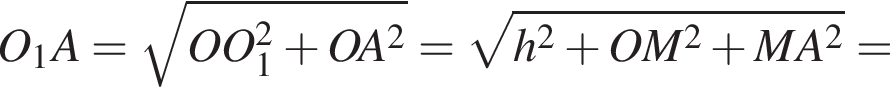
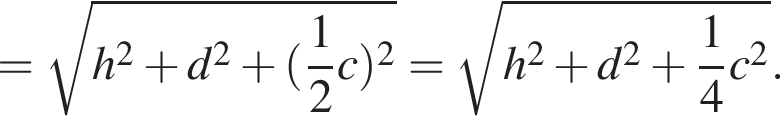
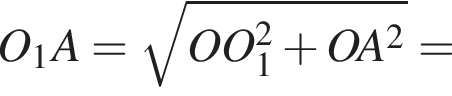
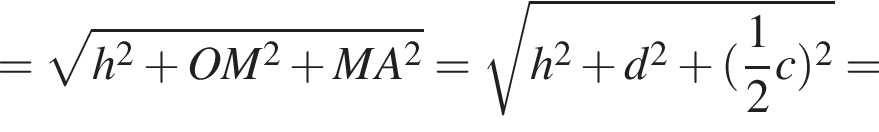
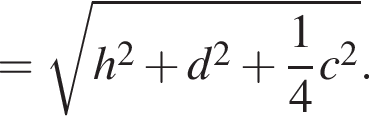

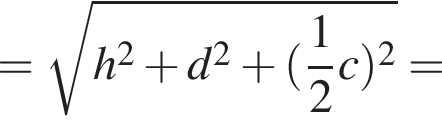
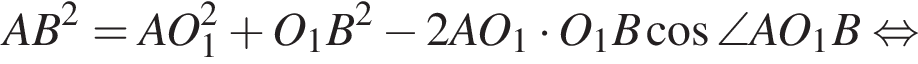
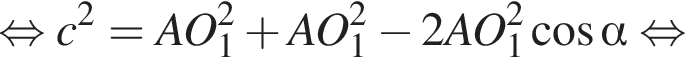
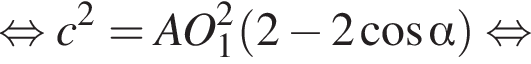
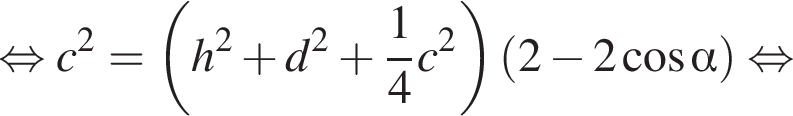
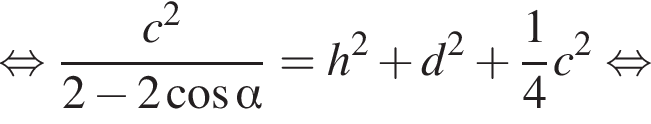
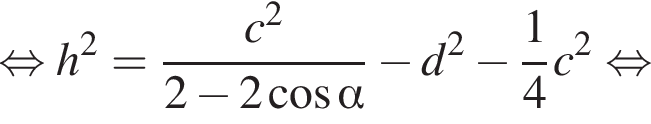
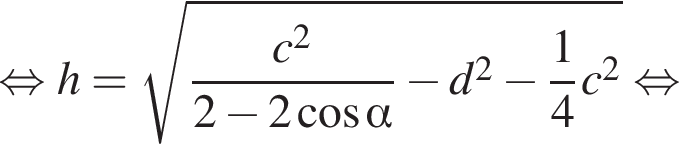
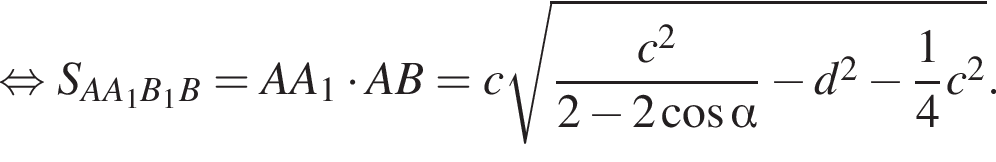
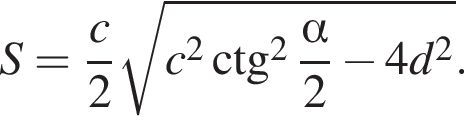
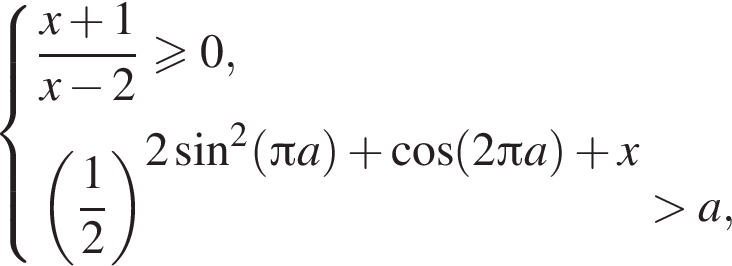
 Во втором неравенстве сначала преобразуем показатель степени. Имеем:
Во втором неравенстве сначала преобразуем показатель степени. Имеем: 

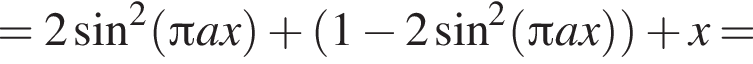
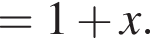
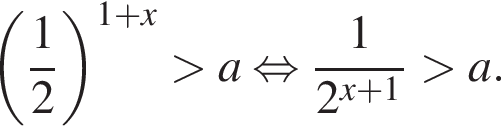
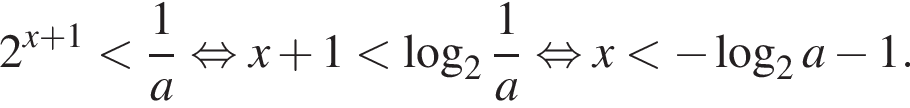
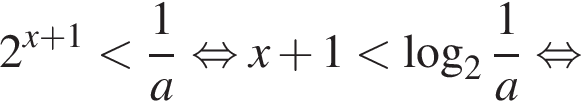
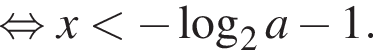
 Значит, нужно выяснить, как соотносится
Значит, нужно выяснить, как соотносится 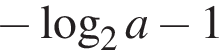 с числами −1 и 2. Решим, например, неравенство
с числами −1 и 2. Решим, например, неравенство 
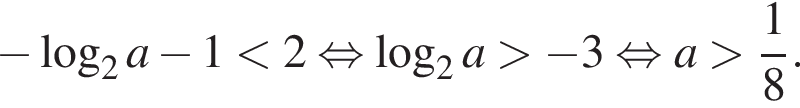
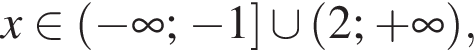 якщо
якщо 
 якщо
якщо 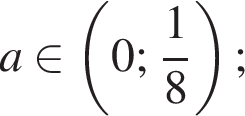
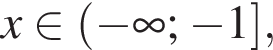 якщо
якщо 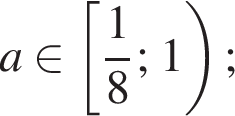
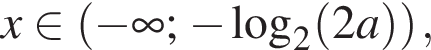 якщо
якщо